- 做项目(多个C++、Java、Go、测开、前端项目) (opens new window)
- 刷算法(两个月高强度学算法) (opens new window)
- 背八股(40天挑战高频面试题) (opens new window)
# 474.一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
- 输入:strs = ["10", "0", "1"], m = 1, n = 1
- 输出:2
- 解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
- 1 <= strs.length <= 600
- 1 <= strs[i].length <= 100
- strs[i] 仅由 '0' 和 '1' 组成
- 1 <= m, n <= 100
# 算法公开课
《代码随想录》算法视频公开课 (opens new window):装满这个背包最多用多少个物品?| LeetCode:474.一和零 (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
# 思路
如果对背包问题不都熟悉先看这两篇:
这道题目,还是比较难的,也有点像程序员自己给自己出个脑筋急转弯,程序员何苦为难程序员呢。
来说题,本题不少同学会认为是多重背包,一些题解也是这么写的。
其实本题并不是多重背包,再来看一下这个图,捋清几种背包的关系
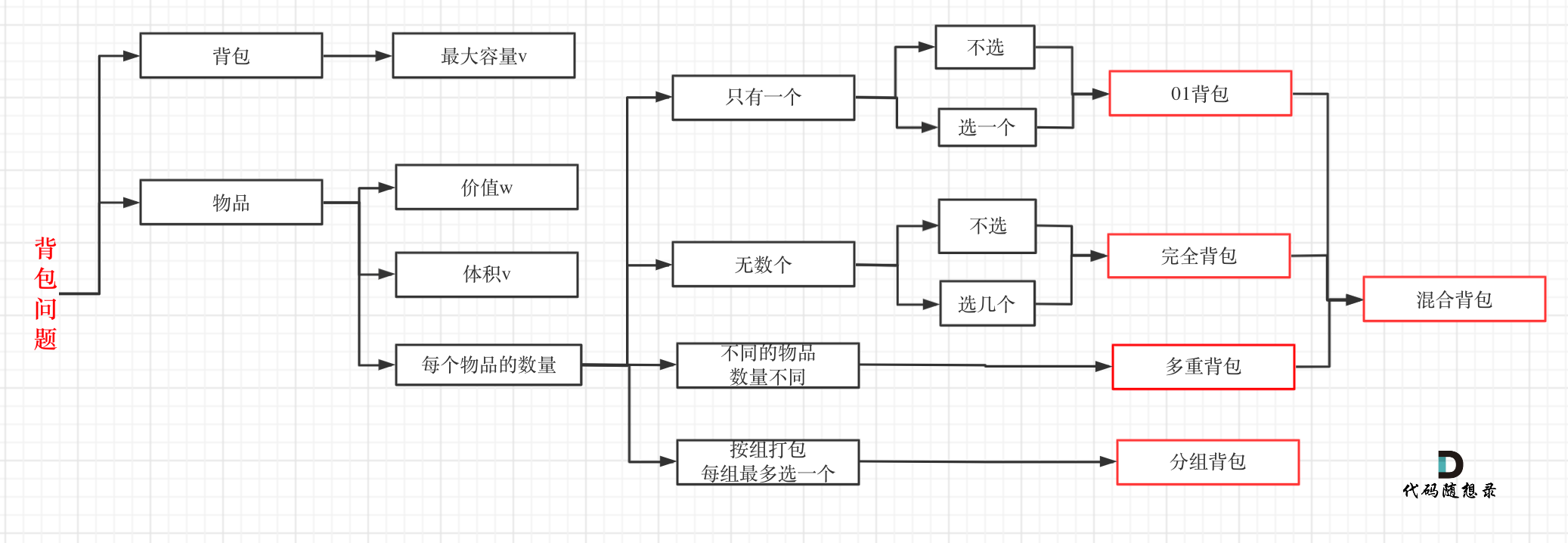
多重背包是每个物品,数量不同的情况。
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
理解成多重背包的同学主要是把m和n混淆为物品了,感觉这是不同数量的物品,所以以为是多重背包。
但本题其实是01背包问题!
只不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
开始动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
- 确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
- dp数组如何初始化
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中已经讲解了,01背包的dp数组初始化为0就可以。
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
- 确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲到了01背包为什么一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
那么本题也是,物品就是strs里的字符串,背包容量就是题目描述中的m和n。
代码如下:
for (string str : strs) { // 遍历物品
int oneNum = 0, zeroNum = 0;
for (char c : str) {
if (c == '0') zeroNum++;
else oneNum++;
}
for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历!
for (int j = n; j >= oneNum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
有同学可能想,那个遍历背包容量的两层for循环先后循序有没有什么讲究?
没讲究,都是物品重量的一个维度,先遍历哪个都行!
- 举例推导dp数组
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
最后dp数组的状态如下所示:
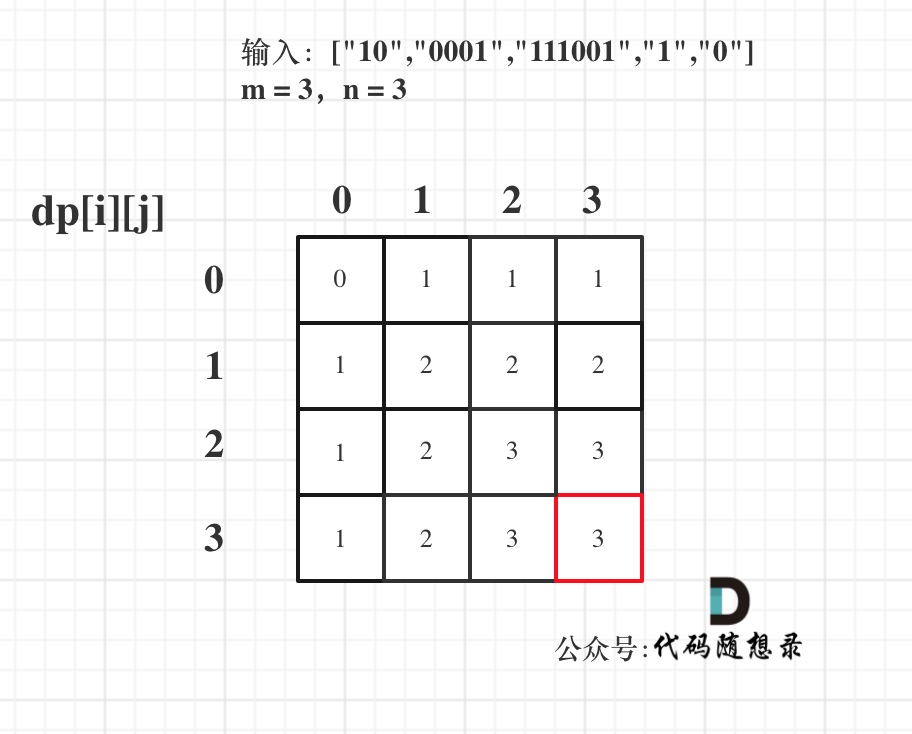
以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
for (string str : strs) { // 遍历物品
int oneNum = 0, zeroNum = 0;
for (char c : str) {
if (c == '0') zeroNum++;
else oneNum++;
}
for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历!
for (int j = n; j >= oneNum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
return dp[m][n];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
- 时间复杂度: O(kmn),k 为strs的长度
- 空间复杂度: O(mn)
C++: 使用三维数组的版本
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int num_of_str = strs.size();
vector<vector<vector<int>>> dp(num_of_str, vector<vector<int>>(m + 1,vector<int>(n + 1, 0)));
/* dp[i][j][k] represents, if choosing items among strs[0] to strs[i] to form a subset,
what is the maximum size of this subset such that there are no more than m 0's and n 1's in this subset.
Each entry of dp[i][j][k] is initialized with 0
transition formula:
using x[i] to indicates the number of 0's in strs[i]
using y[i] to indicates the number of 1's in strs[i]
dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j - x[i]][k - y[i]] + 1)
*/
// num_of_zeros records the number of 0's for each str
// num_of_ones records the number of 1's for each str
// find the number of 0's and the number of 1's for each str in strs
vector<int> num_of_zeros;
vector<int> num_of_ones;
for (auto& str : strs){
int count_of_zero = 0;
int count_of_one = 0;
for (char &c : str){
if(c == '0') count_of_zero ++;
else count_of_one ++;
}
num_of_zeros.push_back(count_of_zero);
num_of_ones.push_back(count_of_one);
}
// num_of_zeros[0] indicates the number of 0's for str[0]
// num_of_ones[0] indiates the number of 1's for str[1]
// initialize the 1st plane of dp[i][j][k], i.e., dp[0][j][k]
// if num_of_zeros[0] > m or num_of_ones[0] > n, no need to further initialize dp[0][j][k],
// because they have been intialized to 0 previously
if(num_of_zeros[0] <= m && num_of_ones[0] <= n){
// for j < num_of_zeros[0] or k < num_of_ones[0], dp[0][j][k] = 0
for(int j = num_of_zeros[0]; j <= m; j++){
for(int k = num_of_ones[0]; k <= n; k++){
dp[0][j][k] = 1;
}
}
}
/* if j - num_of_zeros[i] >= 0 and k - num_of_ones[i] >= 0:
dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j - num_of_zeros[i]][k - num_of_ones[i]] + 1)
else:
dp[i][j][k] = dp[i-1][j][k]
*/
for (int i = 1; i < num_of_str; i++){
int count_of_zeros = num_of_zeros[i];
int count_of_ones = num_of_ones[i];
for (int j = 0; j <= m; j++){
for (int k = 0; k <= n; k++){
if( j < count_of_zeros || k < count_of_ones){
dp[i][j][k] = dp[i-1][j][k];
}else{
dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j - count_of_zeros][k - count_of_ones] + 1);
}
}
}
}
return dp[num_of_str-1][m][n];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
# 总结
不少同学刷过这道题,可能没有总结这究竟是什么背包。
此时我们讲解了0-1背包的多种应用,
- 纯 0 - 1 背包 (opens new window) 是求 给定背包容量 装满背包 的最大价值是多少。
- 416. 分割等和子集 (opens new window) 是求 给定背包容量,能不能装满这个背包。
- 1049. 最后一块石头的重量 II (opens new window) 是求 给定背包容量,尽可能装,最多能装多少
- 494. 目标和 (opens new window) 是求 给定背包容量,装满背包有多少种方法。
- 本题是求 给定背包容量,装满背包最多有多少个物品。
所以在代码随想录中所列举的题目,都是 0-1背包不同维度上的应用,大家可以细心体会!
# 其他语言版本
# Java
三维DP数组实现
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
/// 数组有三个维度
// 第一个维度:取前面的几个字符串
// 第二个维度:0的数量限制(背包维度 1 容量)
// 第三个维度:1的数量限制(背包维度 2 容量)
int[][][] dpArr = new int[strs.length][m + 1][n + 1];
/// 初始化dpArr数组
// 计算第一个字符串的零数量和1数量
int zeroNum = 0;
int oneNum = 0;
for (char c : strs[0].toCharArray()) {
if (c == '0') {
zeroNum++;
} else {
oneNum++;
}
}
// 当0数量、1数量都容得下第一个字符串时,将DP数组的相应位置初始化为1,因为当前的子集数量为1
for (int j = zeroNum; j <= m; j++) {
for (int k = oneNum; k <= n; k++) {
dpArr[0][j][k] = 1;
}
}
/// 依次填充加入第i个字符串之后的DP数组
for (int i = 1; i < strs.length; i++) {
zeroNum = 0;
oneNum = 0;
for (char c : strs[i].toCharArray()) {
if (c == '0') {
zeroNum++;
} else {
oneNum++;
}
}
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if (j >= zeroNum && k >= oneNum) {
// --if-- 当0数量维度和1数量维度的容量都大于等于当前字符串的0数量和1数量时,才考虑是否将当前字符串放入背包
// 不放入第i个字符串,子集数量仍为 dpArr[i - 1][j][k]
// 放入第i个字符串,需要在0维度腾出 zeroNum 个容量,1维度腾出 oneNum 个容量,然后放入当前字符串,即 dpArr[i - 1][j - zeroNum][k - oneNum] + 1)
dpArr[i][j][k] = Math.max(dpArr[i - 1][j][k], dpArr[i - 1][j - zeroNum][k - oneNum] + 1);
} else {
// --if-- 无法放入第i个字符串,子集数量仍为 dpArr[i - 1][j][k]
dpArr[i][j][k] = dpArr[i - 1][j][k];
}
}
}
}
return dpArr[dpArr.length - 1][m][n];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
二维DP数组实现
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
//dp[i][j]表示i个0和j个1时的最大子集
int[][] dp = new int[m + 1][n + 1];
int oneNum, zeroNum;
for (String str : strs) {
oneNum = 0;
zeroNum = 0;
for (char ch : str.toCharArray()) {
if (ch == '0') {
zeroNum++;
} else {
oneNum++;
}
}
//倒序遍历
for (int i = m; i >= zeroNum; i--) {
for (int j = n; j >= oneNum; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
return dp[m][n];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Python
DP(版本一)
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
dp = [[0] * (n + 1) for _ in range(m + 1)] # 创建二维动态规划数组,初始化为0
for s in strs: # 遍历物品
zeroNum = s.count('0') # 统计0的个数
oneNum = len(s) - zeroNum # 统计1的个数
for i in range(m, zeroNum - 1, -1): # 遍历背包容量且从后向前遍历
for j in range(n, oneNum - 1, -1):
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1) # 状态转移方程
return dp[m][n]
2
3
4
5
6
7
8
9
10
11
DP(版本二)
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
dp = [[0] * (n + 1) for _ in range(m + 1)] # 创建二维动态规划数组,初始化为0
# 遍历物品
for s in strs:
ones = s.count('1') # 统计字符串中1的个数
zeros = s.count('0') # 统计字符串中0的个数
# 遍历背包容量且从后向前遍历
for i in range(m, zeros - 1, -1):
for j in range(n, ones - 1, -1):
dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1) # 状态转移方程
return dp[m][n]
2
3
4
5
6
7
8
9
10
11
12
13
# Go
func findMaxForm(strs []string, m int, n int) int {
// 定义数组
dp := make([][]int, m+1)
for i,_ := range dp {
dp[i] = make([]int, n+1 )
}
// 遍历
for i:=0;i<len(strs);i++ {
zeroNum,oneNum := 0 , 0
//计算0,1 个数
//或者直接strings.Count(strs[i],"0")
for _,v := range strs[i] {
if v == '0' {
zeroNum++
}
}
oneNum = len(strs[i])-zeroNum
// 从后往前 遍历背包容量
for j:= m ; j >= zeroNum;j-- {
for k:=n ; k >= oneNum;k-- {
// 推导公式
dp[j][k] = max(dp[j][k],dp[j-zeroNum][k-oneNum]+1)
}
}
//fmt.Println(dp)
}
return dp[m][n]
}
func max(a,b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# JavaScript
const findMaxForm = (strs, m, n) => {
const dp = Array.from(Array(m+1), () => Array(n+1).fill(0));
let numOfZeros, numOfOnes;
for(let str of strs) {
numOfZeros = 0;
numOfOnes = 0;
for(let c of str) {
if (c === '0') {
numOfZeros++;
} else {
numOfOnes++;
}
}
for(let i = m; i >= numOfZeros; i--) {
for(let j = n; j >= numOfOnes; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - numOfZeros][j - numOfOnes] + 1);
}
}
}
return dp[m][n];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# TypeScript
滚动数组,二维数组法
type BinaryInfo = { numOfZero: number, numOfOne: number };
function findMaxForm(strs: string[], m: number, n: number): number {
const goodsNum: number = strs.length;
const dp: number[][] = new Array(m + 1).fill(0)
.map(_ => new Array(n + 1).fill(0));
for (let i = 0; i < goodsNum; i++) {
const { numOfZero, numOfOne } = countBinary(strs[i]);
for (let j = m; j >= numOfZero; j--) {
for (let k = n; k >= numOfOne; k--) {
dp[j][k] = Math.max(dp[j][k], dp[j - numOfZero][k - numOfOne] + 1);
}
}
}
return dp[m][n];
};
function countBinary(str: string): BinaryInfo {
let numOfZero: number = 0,
numOfOne: number = 0;
for (let s of str) {
if (s === '0') {
numOfZero++;
} else {
numOfOne++;
}
}
return { numOfZero, numOfOne };
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
传统背包,三维数组法
type BinaryInfo = { numOfZero: number, numOfOne: number };
function findMaxForm(strs: string[], m: number, n: number): number {
/**
dp[i][j][k]: 前i个物品中, 背包的0容量为j, 1容量为k, 最多能放的物品数量
*/
const goodsNum: number = strs.length;
const dp: number[][][] = new Array(goodsNum).fill(0)
.map(_ => new Array(m + 1)
.fill(0)
.map(_ => new Array(n + 1).fill(0))
);
const { numOfZero, numOfOne } = countBinary(strs[0]);
for (let i = numOfZero; i <= m; i++) {
for (let j = numOfOne; j <= n; j++) {
dp[0][i][j] = 1;
}
}
for (let i = 1; i < goodsNum; i++) {
const { numOfZero, numOfOne } = countBinary(strs[i]);
for (let j = 0; j <= m; j++) {
for (let k = 0; k <= n; k++) {
if (j < numOfZero || k < numOfOne) {
dp[i][j][k] = dp[i - 1][j][k];
} else {
dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - numOfZero][k - numOfOne] + 1);
}
}
}
}
return dp[dp.length - 1][m][n];
};
function countBinary(str: string): BinaryInfo {
let numOfZero: number = 0,
numOfOne: number = 0;
for (let s of str) {
if (s === '0') {
numOfZero++;
} else {
numOfOne++;
}
}
return { numOfZero, numOfOne };
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
回溯法(会超时)
function findMaxForm(strs: string[], m: number, n: number): number {
/**
思路:暴力枚举strs的所有子集,记录符合条件子集的最大长度
*/
let resMax: number = 0;
backTrack(strs, m, n, 0, []);
return resMax;
function backTrack(
strs: string[], m: number, n: number,
startIndex: number, route: string[]
): void {
if (startIndex === strs.length) return;
for (let i = startIndex, length = strs.length; i < length; i++) {
route.push(strs[i]);
if (isValidSubSet(route, m, n)) {
resMax = Math.max(resMax, route.length);
backTrack(strs, m, n, i + 1, route);
}
route.pop();
}
}
};
function isValidSubSet(strs: string[], m: number, n: number): boolean {
let zeroNum: number = 0,
oneNum: number = 0;
strs.forEach(str => {
for (let s of str) {
if (s === '0') {
zeroNum++;
} else {
oneNum++;
}
}
});
return zeroNum <= m && oneNum <= n;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Scala
背包:
object Solution {
def findMaxForm(strs: Array[String], m: Int, n: Int): Int = {
var dp = Array.ofDim[Int](m + 1, n + 1)
var (oneNum, zeroNum) = (0, 0)
for (str <- strs) {
oneNum = 0
zeroNum = 0
for (i <- str.indices) {
if (str(i) == '0') zeroNum += 1
else oneNum += 1
}
for (i <- m to zeroNum by -1) {
for (j <- n to oneNum by -1) {
dp(i)(j) = math.max(dp(i)(j), dp(i - zeroNum)(j - oneNum) + 1)
}
}
}
dp(m)(n)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
回溯法(超时):
object Solution {
import scala.collection.mutable
var res = Int.MinValue
def test(str: String): (Int, Int) = {
var (zero, one) = (0, 0)
for (i <- str.indices) {
if (str(i) == '1') one += 1
else zero += 1
}
(zero, one)
}
def travsel(strs: Array[String], path: mutable.ArrayBuffer[String], m: Int, n: Int, startIndex: Int): Unit = {
if (startIndex > strs.length) {
return
}
res = math.max(res, path.length)
for (i <- startIndex until strs.length) {
var (zero, one) = test(strs(i))
// 如果0的个数小于m,1的个数小于n,则可以回溯
if (zero <= m && one <= n) {
path.append(strs(i))
travsel(strs, path, m - zero, n - one, i + 1)
path.remove(path.length - 1)
}
}
}
def findMaxForm(strs: Array[String], m: Int, n: Int): Int = {
res = Int.MinValue
var path = mutable.ArrayBuffer[String]()
travsel(strs, path, m, n, 0)
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# Rust
impl Solution {
pub fn find_max_form(strs: Vec<String>, m: i32, n: i32) -> i32 {
let (m, n) = (m as usize, n as usize);
let mut dp = vec![vec![0; n + 1]; m + 1];
for s in strs {
let (mut one_num, mut zero_num) = (0, 0);
for c in s.chars() {
match c {
'0' => zero_num += 1,
'1' => one_num += 1,
_ => (),
}
}
for i in (zero_num..=m).rev() {
for j in (one_num..=n).rev() {
dp[i][j] = dp[i][j].max(dp[i - zero_num][j - one_num] + 1);
}
}
}
dp[m][n]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C
#define max(a, b) ((a) > (b) ? (a) : (b))
int findMaxForm(char** strs, int strsSize, int m, int n) {
int dp[m + 1][n + 1];
memset(dp, 0, sizeof (int ) * (m + 1) * (n + 1));
for(int i = 0; i < strsSize; i++){
// 统计0和1的数量
int count0 = 0;
int count1 = 0;
char *str = strs[i];
while (*str != '\0'){
if(*str == '0'){
count0++;
} else{
count1++;
}
str++;
}
for(int j = m; j >= count0; j--){
for(int k = n; k >= count1; k--){
dp[j][k] = max(dp[j][k], dp[j - count0][k - count1] + 1);
}
}
}
return dp[m][n];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# C#
public class Solution
{
public int FindMaxForm(string[] strs, int m, int n)
{
int[,] dp = new int[m + 1, n + 1];
foreach (string str in strs)
{
int zero = 0, one = 0;
foreach (char c in str)
{
if (c == '0') zero++;
else one++;
}
for (int i = m; i >= zero; i--)
{
for (int j = n; j >= one; j--)
{
dp[i, j] = Math.Max(dp[i, j], dp[i - zero, j - one] + 1);
}
}
}
return dp[m, n];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
← 16. 目标和 18. 完全背包理论基础 →
