A * 算法精讲 （A star算法）

卡码网：126. 骑士的攻击 (opens new window)

题目描述

在象棋中，马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标，要求根据骑士的移动规则，计算从起点到达目标点所需的最短步数。

骑士移动规则如图，红色是起始位置，黄色是骑士可以走的地方。

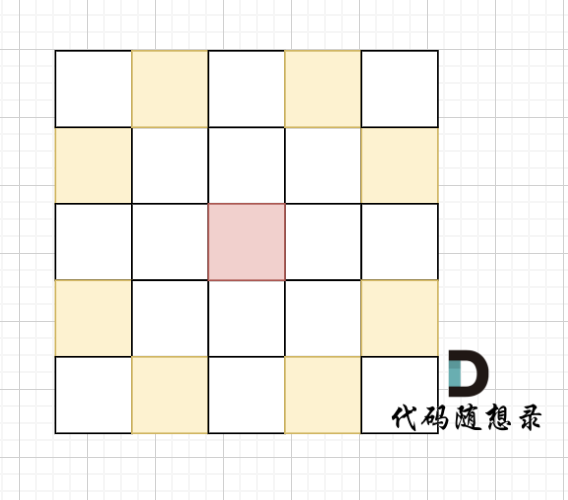
棋盘大小 1000 x 1000（棋盘的 x 和 y 坐标均在 [1, 1000] 区间内，包含边界）

输入描述

第一行包含一个整数 n，表示测试用例的数量。

接下来的 n 行，每行包含四个整数 a1, a2, b1, b2，分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。

输出描述

输出共 n 行，每行输出一个整数，表示骑士从起点到目标点的最短路径长度。

输入示例

6
5 2 5 4
1 1 2 2
1 1 8 8
1 1 8 7
2 1 3 3
4 6 4 6

输出示例

2
4
6
5
1
0

思路

我们看到这道题目的第一个想法就是广搜，这也是最经典的广搜类型题目。

这里我直接给出广搜的C++代码：

#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
int moves[1001][1001];
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
void bfs(int a1,int a2, int b1, int b2)
{
	queue<int> q;
	q.push(a1);
	q.push(a2);
	while(!q.empty())
	{
		int m=q.front(); q.pop();
		int n=q.front(); q.pop();
		if(m == b1 && n == b2)
		break;
		for(int i=0;i<8;i++)
		{
			int mm=m + dir[i][0];
			int nn=n + dir[i][1];
			if(mm < 1 || mm > 1000 || nn < 1 || nn > 1000)
			continue;
			if(!moves[mm][nn])
			{
				moves[mm][nn]=moves[m][n]+1;
				q.push(mm);
				q.push(nn);
			}
		}
	}
}

int main()
{
    int n, a1, a2, b1, b2;
    cin >> n;
    while (n--) {
        cin >> a1 >> a2 >> b1 >> b2;
        memset(moves,0,sizeof(moves));
		bfs(a1, a2, b1, b2);
		cout << moves[b1][b2] << endl;
	}
	return 0;
}

提交后，大家会发现，超时了。

因为本题地图足够大，且 n 也有可能很大，导致有非常多的查询。

我们来看一下广搜的搜索过程，如图，红色是起点，绿色是终点，黄色是要遍历的点，最后从 起点 找到 达到终点的最短路径是棕色。

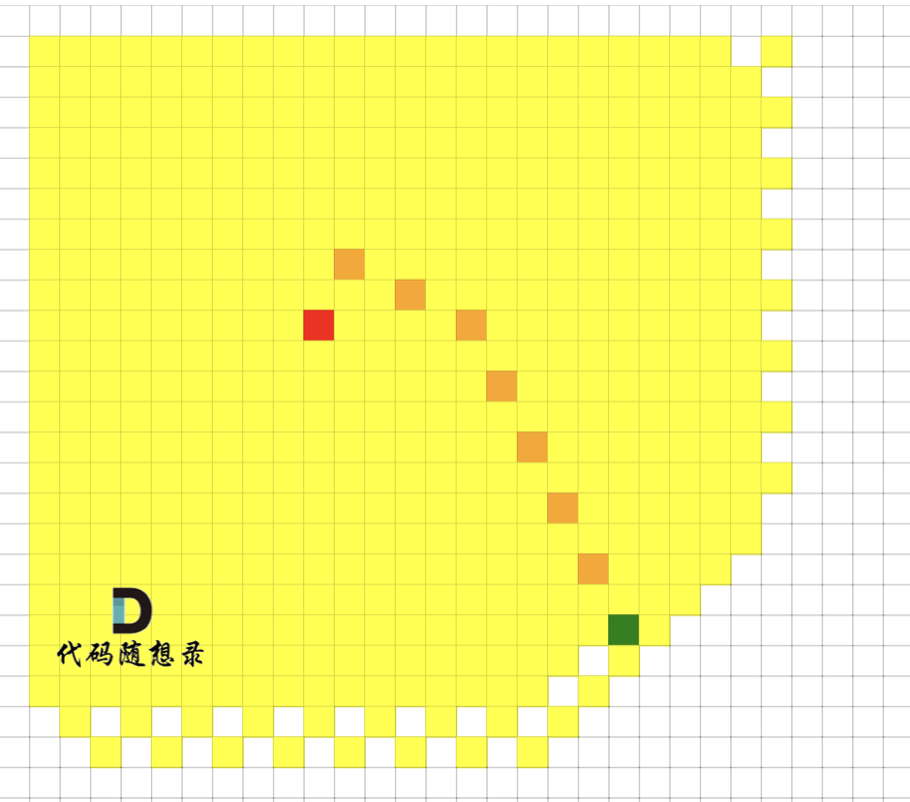
可以看出 广搜中，做了很多无用的遍历， 黄色的格子是广搜遍历到的点。

这里我们能不能让便利方向，向这终点的方向去遍历呢？

这样我们就可以避免很多无用遍历。

Astar

Astar 是一种 广搜的改良版。 有的是 Astar是 dijkstra 的改良版。

其实只是场景不同而已 我们在搜索最短路的时候， 如果是无权图（边的权值都是1） 那就用广搜，代码简洁，时间效率和 dijkstra 差不多 （具体要取决于图的稠密）

如果是有权图（边有不同的权值），优先考虑 dijkstra。

而 Astar 关键在于 启发式函数， 也就是 影响 广搜或者 dijkstra 从 容器（队列）里取元素的优先顺序。

以下，我用BFS版本的A * 来进行讲解。

在BFS中，我们想搜索，从起点到终点的最短路径，要一层一层去遍历。

如果 使用A * 的话，其搜索过程是这样的，如图，图中着色的都是我们要遍历的点。

（上面两图中 最短路长度都是8，只是走的方式不同而已）

大家可以发现 BFS 是没有目的性的 一圈一圈去搜索， 而 A * 是有方向性的去搜索。

看出 A * 可以节省很多没有必要的遍历步骤。

为了让大家可以明显看到区别，我将 BFS 和 A * 制作成可视化动图，大家可以自己看看动图，效果更好。

地址：https://kamacoder.com/tools/knight.html

那么 A * 为什么可以有方向性的去搜索，它的如何知道方向呢？

其关键在于 启发式函数。

那么启发式函数落实到代码处，如果指引搜索的方向？

在本篇开篇中给出了BFS代码，指引 搜索的方向的关键代码在这里：

int m=q.front();q.pop();
int n=q.front();q.pop();

从队列里取出什么元素，接下来就是从哪里开始搜索。

所以 启发式函数 要影响的就是队列里元素的排序！

这是影响BFS搜索方向的关键。

对队列里节点进行排序，就需要给每一个节点权值，如何计算权值呢？

每个节点的权值为F，给出公式为：F = G + H

G：起点达到目前遍历节点的距离

H：目前遍历的节点到达终点的距离

起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。

本题的图是无权网格状，在计算两点距离通常有如下三种计算方式：

1. 曼哈顿距离，计算方式： d = abs(x1-x2)+abs(y1-y2)
2. 欧氏距离（欧拉距离） ，计算方式：d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
3. 切比雪夫距离，计算方式：d = max(abs(x1 - x2), abs(y1 - y2))

x1, x2 为起点坐标，y1, y2 为终点坐标 ，abs 为求绝对值，sqrt 为求开根号，

选择哪一种距离计算方式 也会导致 A * 算法的结果不同。

本题，采用欧拉距离才能最大程度体现 点与点之间的距离。

所以 使用欧拉距离计算 和 广搜搜出来的最短路的节点数是一样的。 （路径可能不同，但路径上的节点数是相同的）

我在制作动画演示的过程中，分别给出了曼哈顿、欧拉以及契比雪夫 三种计算方式下，A * 算法的寻路过程，大家可以自己看看看其区别。

动画地址：https://kamacoder.com/tools/knight.html

计算出来 F 之后，按照 F 的 大小，来选去出队列的节点。

可以使用 优先级队列 帮我们排好序，每次出队列，就是F最小的节点。

实现代码如下：（启发式函数 采用 欧拉距离计算方式）

#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
int moves[1001][1001];
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
int b1, b2;
// F = G + H
// G = 从起点到该节点路径消耗
// H = 该节点到终点的预估消耗

struct Knight{
    int x,y;
    int g,h,f;
    bool operator < (const Knight & k) const{  // 重载运算符， 从小到大排序
     return k.f < f;
    }
};

priority_queue<Knight> que;

int Heuristic(const Knight& k) { // 欧拉距离
    return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号，这样可以提高精度
}
void astar(const Knight& k)
{
    Knight cur, next;
	que.push(k);
	while(!que.empty())
	{
		cur=que.top(); que.pop();
		if(cur.x == b1 && cur.y == b2)
		break;
		for(int i = 0; i < 8; i++)
		{
			next.x = cur.x + dir[i][0];
			next.y = cur.y + dir[i][1];
			if(next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000)
			continue;
			if(!moves[next.x][next.y])
			{
				moves[next.x][next.y] = moves[cur.x][cur.y] + 1;

                // 开始计算F
				next.g = cur.g + 5; // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5
                next.h = Heuristic(next);
                next.f = next.g + next.h;
                que.push(next);
			}
		}
	}
}

int main()
{
    int n, a1, a2;
    cin >> n;
    while (n--) {
        cin >> a1 >> a2 >> b1 >> b2;
        memset(moves,0,sizeof(moves));
        Knight start;
        start.x = a1;
        start.y = a2;
        start.g = 0;
        start.h = Heuristic(start);
        start.f = start.g + start.h;
		astar(start);
        while(!que.empty()) que.pop(); // 队列清空
		cout << moves[b1][b2] << endl;
	}
	return 0;
}

复杂度分析

A * 算法的时间复杂度 其实是不好去量化的，因为他取决于 启发式函数怎么写。

最坏情况下，A * 退化成广搜，算法的时间复杂度 是 O(n * 2)，n 为节点数量。

最佳情况，是从起点直接到终点，时间复杂度为 O(dlogd)，d 为起点到终点的深度。

因为在搜索的过程中也需要堆排序，所以是 O(dlogd)。

实际上 A * 的时间复杂度是介于 最优 和最坏 情况之间， 可以 非常粗略的认为 A * 算法的时间复杂度是 O(nlogn) ，n 为节点数量。

A * 算法的空间复杂度 O(b ^ d) ,d 为起点到终点的深度，b 是 图中节点间的连接数量，本题因为是无权网格图，所以 节点间连接数量为 4。

拓展

如果本题大家使用 曼哈顿距离 或者 切比雪夫距离 计算的话，可以提交试一试，有的最短路结果是并不是最短的。

原因也是 曼哈顿 和 切比雪夫这两种计算方式在 本题的网格地图中，都没有体现出点到点的真正距离！

可能有些录友找到类似的题目，例如 poj 2243 (opens new window)，使用 曼哈顿距离 提交也过了， 那是因为题目中的地图太小了，仅仅是一张 8 * 8的地图，根本看不出来 不同启发式函数写法的区别。

A * 算法 并不是一个明确的最短路算法，A * 算法搜的路径如何，完全取决于 启发式函数怎么写。

A * 算法并不能保证一定是最短路，因为在设计 启发式函数的时候，要考虑 时间效率与准确度之间的一个权衡。

虽然本题中，A * 算法得到是最短路，也是因为本题 启发式函数 和 地图结构都是最简单的。

例如在游戏中，在地图很大、不同路径权值不同、有障碍 且多个游戏单位在地图中寻路的情况，如果要计算准确最短路，耗时很大，会给玩家一种卡顿的感觉。

而真实玩家在玩游戏的时候，并不要求一定是最短路，次短路也是可以的 （玩家不一定能感受出来，及时感受出来也不是很在意），只要奔着目标走过去 大体就可以接受。

所以 在游戏开发设计中，保证运行效率的情况下，A * 算法中的启发式函数 设计往往不是最短路，而是接近最短路的 次短路设计。

大家如果玩 LOL，或者 王者荣耀 可以回忆一下：如果 从很远的地方点击 让英雄直接跑过去 是 跑的路径是不靠谱的，所以玩家们才会在 距离英雄尽可能近的位置去点击 让英雄跑过去。

A * 的缺点

大家看上述 A * 代码的时候，可以看到 我们想 队列里添加了很多节点，但真正从队列里取出来的 仅仅是 靠启发式函数判断 距离终点最近的节点。

相对了 普通BFS，A * 算法只从 队列里取出 距离终点最近的节点。

那么问题来了，A * 在一次路径搜索中，大量不需要访问的节点都在队列里，会造成空间的过度消耗。

IDA * 算法 对这一空间增长问题进行了优化，关于 IDA * 算法，本篇不再做讲解，感兴趣的录友可以自行找资料学习。

另外还有一种场景 是 A * 解决不了的。

如果题目中，给出 多个可能的目标，然后在这多个目标中 选择最近的目标，这种 A * 就不擅长了， A * 只擅长给出明确的目标 然后找到最短路径。

如果是多个目标找最近目标（特别是潜在目标数量很多的时候），可以考虑 Dijkstra ，BFS 或者 Floyd。

其他语言版本

Java

Python

import heapq
 
n = int(input())
 
moves = [(1, 2), (2, 1), (-1, 2), (2, -1), (1, -2), (-2, 1), (-1, -2), (-2, -1)]
 
def distance(a, b):
    return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** 0.5
 
def bfs(start, end):
    q = [(distance(start, end), start)]
    step = {start: 0}
     
    while q:
        d, cur = heapq.heappop(q)
        if cur == end:
            return step[cur]
        for move in moves:
            new = (move[0] + cur[0], move[1] + cur[1])
            if 1 <= new[0] <= 1000 and 1 <= new[1] <= 1000:
                step_new = step[cur] + 1
                if step_new < step.get(new, float('inf')):
                    step[new] = step_new
                    heapq.heappush(q, (distance(new, end) + step_new, new))
    return False
                     
for _ in range(n):
    a1, a2, b1, b2 = map(int, input().split())
    print(bfs((a1, a2), (b1, b2)))

Go

Rust

JavaScript

class MinHeap {
  constructor() {
    this.val = []
  }
  push(val) {
    this.val.push(val)
    if (this.val.length > 1) {
      this.bubbleUp()
    }
  }
  bubbleUp() {
    let pi = this.val.length - 1
    let pp = Math.floor((pi - 1) / 2)
    while (pi > 0 && this.val[pp][0] > this.val[pi][0]) {
      ;[this.val[pi], this.val[pp]] = [this.val[pp], this.val[pi]]
      pi = pp
      pp = Math.floor((pi - 1) / 2)
    }
  }
  pop() {
    if (this.val.length > 1) {
        let pp = 0
        let pi = this.val.length - 1
        ;[this.val[pi], this.val[pp]] = [this.val[pp], this.val[pi]]
        const min = this.val.pop()
        if (this.val.length > 1) {
          this.sinkDown(0)
        }
        return min        
    } else if (this.val.length == 1) {
        return this.val.pop()
    }

  }
  sinkDown(parentIdx) {
    let pp = parentIdx
    let plc = pp * 2 + 1
    let prc = pp * 2 + 2
    let pt = pp // temp pointer
    if (plc < this.val.length && this.val[pp][0] > this.val[plc][0]) {
        pt = plc
    }
    if (prc < this.val.length && this.val[pt][0] > this.val[prc][0]) {
        pt = prc
    }
    if (pt != pp) {
        ;[this.val[pp], this.val[pt]] = [this.val[pt], this.val[pp]]
        this.sinkDown(pt)
    }
  }
}

const moves = [
    [1, 2], 
    [2, 1], 
    [-1, -2], 
    [-2, -1],
    [-1, 2], 
    [-2, 1],
    [1, -2], 
    [2, -1]
]

function dist(a, b) {
    return ((a[0] - b[0])**2 + (a[1] - b[1])**2)**0.5
}

function isValid(x, y) {
    return x >= 1 && y >= 1 && x < 1001 && y < 1001
}

function bfs(start, end) {
    const step = new Map()
    step.set(start.join(" "), 0)
    const q = new MinHeap()
    q.push([dist(start, end), start[0], start[1]])
    
    while(q.val.length) {
        const [d, x, y] = q.pop()
        // if x and y correspond to end position output result
        if (x == end[0] && y == end[1]) {
            console.log(step.get(end.join(" ")))
            break;
        }
        for (const [dx, dy] of moves) {
            const nx = dx + x
            const ny = dy + y
            if (isValid(nx, ny)) {
                const newStep = step.get([x, y].join(" ")) + 1
                const newDist = dist([nx, ny], [...end])
                const s = step.get([nx, ny].join(" ")) ? 
                    step.get([nx, ny]) : 
                    Number.MAX_VALUE
                if (newStep < s) {
                    q.push(
                        [
                            newStep + newDist, 
                            nx, 
                            ny
                        ]
                    )
                    step.set([nx, ny].join(" "), newStep)
                } 
            }
        }
    }
}

async function main() {
    const rl = require('readline').createInterface({ input: process.stdin })
    const iter = rl[Symbol.asyncIterator]()
    const readline = async () => (await iter.next()).value
    const n = Number((await readline()))
    
    // find min step
    for (let i = 0 ; i < n ; i++) {
        const [s1, s2, t1, t2] = (await readline()).split(" ").map(Number)
        bfs([s1, s2], [t1, t2])
    }
}

main()

TypeScript

PhP

Swift

Scala

C#

Dart

C

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 定义一个结构体，表示棋盘上骑士的位置和相关的 A* 算法参数
typedef struct {
    int x, y; // 骑士在棋盘上的坐标
    int g;    // 从起点到当前节点的实际消耗
    int h;    // 从当前节点到目标节点的估计消耗（启发式函数值）
    int f;    // 总的估计消耗（f = g + h）
} Knight;

#define MAX_HEAP_SIZE 2000000 // 假设优先队列的最大容量

// 定义一个优先队列，使用最小堆来实现 A* 算法中的 Open 列表
typedef struct {
    Knight data[MAX_HEAP_SIZE];
    int size;
} PriorityQueue;

// 初始化优先队列
void initQueue(PriorityQueue *pq) {
    pq->size = 0;
}

// 将骑士节点插入优先队列
void push(PriorityQueue *pq, Knight k) {
    if (pq->size >= MAX_HEAP_SIZE) {
        // 堆已满，无法插入新节点
        return;
    }
    int i = pq->size++;
    pq->data[i] = k;
    // 上滤操作，维护最小堆的性质，使得 f 值最小的节点在堆顶
    while (i > 0) {
        int parent = (i - 1) / 2;
        if (pq->data[parent].f <= pq->data[i].f) {
            break;
        }
        // 交换父节点和当前节点
        Knight temp = pq->data[parent];
        pq->data[parent] = pq->data[i];
        pq->data[i] = temp;
        i = parent;
    }
}

// 从优先队列中弹出 f 值最小的骑士节点
Knight pop(PriorityQueue *pq) {
    Knight min = pq->data[0];
    pq->size--;
    pq->data[0] = pq->data[pq->size];
    // 下滤操作，维护最小堆的性质
    int i = 0;
    while (1) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int smallest = i;
        if (left < pq->size && pq->data[left].f < pq->data[smallest].f) {
            smallest = left;
        }
        if (right < pq->size && pq->data[right].f < pq->data[smallest].f) {
            smallest = right;
        }
        if (smallest == i) {
            break;
        }
        // 交换当前节点与最小子节点
        Knight temp = pq->data[smallest];
        pq->data[smallest] = pq->data[i];
        pq->data[i] = temp;
        i = smallest;
    }
    return min;
}

// 判断优先队列是否为空
int isEmpty(PriorityQueue *pq) {
    return pq->size == 0;
}

// 启发式函数：计算从当前位置到目标位置的欧几里得距离的平方（避免开方，提高效率）
int heuristic(int x, int y, int goal_x, int goal_y) {
    int dx = x - goal_x;
    int dy = y - goal_y;
    return dx * dx + dy * dy; // 欧几里得距离的平方
}

// 用于记录从起点到棋盘上每个位置的最小移动次数
int moves[1001][1001];

// 骑士在棋盘上的8个可能移动方向
int dir[8][2] = {
    {-2, -1}, {-2, 1}, {-1, 2}, {1, 2},
    {2, 1}, {2, -1}, {1, -2}, {-1, -2}
};

// 使用 A* 算法寻找从起点到目标点的最短路径
int astar(int start_x, int start_y, int goal_x, int goal_y) {
    PriorityQueue pq;
    initQueue(&pq);

    // 初始化 moves 数组，-1 表示未访问过的位置
    memset(moves, -1, sizeof(moves));
    moves[start_x][start_y] = 0; // 起点位置的移动次数为 0

    // 初始化起始节点
    Knight start;
    start.x = start_x;
    start.y = start_y;
    start.g = 0; 
    start.h = heuristic(start_x, start_y, goal_x, goal_y);
    start.f = start.g + start.h; // 总的估计消耗

    push(&pq, start); // 将起始节点加入优先队列

    while (!isEmpty(&pq)) {
        Knight current = pop(&pq); // 取出 f 值最小的节点

        // 如果已经到达目标位置，返回所需的最小移动次数
        if (current.x == goal_x && current.y == goal_y) {
            return moves[current.x][current.y];
        }

        // 遍历当前节点的所有可能移动方向
        for (int i = 0; i < 8; i++) {
            int nx = current.x + dir[i][0];
            int ny = current.y + dir[i][1];

            // 检查新位置是否在棋盘范围内且未被访问过
            if (nx >= 1 && nx <= 1000 && ny >= 1 && ny <= 1000 && moves[nx][ny] == -1) {
                moves[nx][ny] = moves[current.x][current.y] + 1; // 更新移动次数

                // 创建新节点，表示骑士移动到的新位置
                Knight neighbor;
                neighbor.x = nx;
                neighbor.y = ny;
                neighbor.g = current.g + 5; // 每次移动的消耗为 5（骑士移动的距离平方）
                neighbor.h = heuristic(nx, ny, goal_x, goal_y);
                neighbor.f = neighbor.g + neighbor.h;

                push(&pq, neighbor); // 将新节点加入优先队列
            }
        }
    }

    return -1; // 如果无法到达目标位置，返回 -1
}

int main() {
    int n; 
    scanf("%d", &n);
    while (n--) {
        int a1, a2, b1, b2; // 起点和目标点的坐标
        scanf("%d %d %d %d", &a1, &a2, &b1, &b2);

        int result = astar(a1, a2, b1, b2); // 使用 A* 算法计算最短路径
        printf("%d\n", result); // 输出最小移动次数
    }
    return 0;
}