参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！
# Bellman_ford 算法精讲
卡码网：94. 城市间货物运输 I (opens new window)
题目描述
某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。
网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。
权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。
请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。
如果最低运输成本是一个负数，它表示在遵循最优路径的情况下，运输过程中反而能够实现盈利。
城市 1 到城市 n 之间可能会出现没有路径的情况，同时保证道路网络中不存在任何负权回路。
负权回路是指一系列道路的总权值为负，这样的回路使得通过反复经过回路中的道路，理论上可以无限地减少总成本或无限地增加总收益。
输入描述
第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v（单向图）。
输出描述
如果能够从城市 1 到连通到城市 n， 请输出一个整数，表示运输成本。如果该整数是负数，则表示实现了盈利。如果从城市 1 没有路径可达城市 n，请输出 "unconnected"。
输入示例：
6 7
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5
2
3
4
5
6
7
8
# 思路
本题依然是单源最短路问题，求 从 节点1 到节点n 的最小费用。 但本题不同之处在于 边的权值是有负数了。
从 节点1 到节点n 的最小费用也可以是负数，费用如果是负数 则表示 运输的过程中 政府补贴大于运输成本。
在求单源最短路的方法中，使用dijkstra 的话，则要求图中边的权值都为正数。
我们在 dijkstra朴素版 中专门有讲解：为什么有边为负数 使用dijkstra就不行了。
本题是经典的带负权值的单源最短路问题，此时就轮到Bellman_ford登场了，接下来我们来详细介绍Bellman_ford 算法 如何解决这类问题。
该算法是由 R.Bellman 和L.Ford 在20世纪50年代末期发明的算法，故称为Bellman_ford算法。
Bellman_ford算法的核心思想是 对所有边进行松弛n-1次操作（n为节点数量），从而求得目标最短路。
# 什么叫做松弛
看到这里，估计大家都比较晕了，为什么是 n-1 次，那“松弛”这两个字究竟是个啥意思？
我们先来说什么是 “松弛”。
《算法四》里面把这个操作叫做 “放松”， 英文版里叫做 “relax the edge”
所以大家翻译过来，就是 “放松” 或者 “松弛” 。
但《算法四》没有具体去讲这个 “放松” 究竟是个啥？ 网上很多题解也没有讲题解里的 “松弛这条边，松弛所有边”等等 里面的 “松弛” 究竟是什么意思？
这里我给大家举一个例子，每条边有起点、终点和边的权值。例如一条边，节点A 到 节点B 权值为value，如图：
minDist[B] 表示 到达B节点 最小权值，minDist[B] 有哪些状态可以推出来？
状态一： minDist[A] + value 可以推出 minDist[B] 状态二： minDist[B]本身就有权值 （可能是其他边链接的节点B 例如节点C，以至于 minDist[B]记录了其他边到minDist[B]的权值）
minDist[B] 应为如何取舍。
本题我们要求最小权值，那么 这两个状态我们就取最小的
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
2
也就是说，如果 通过 A 到 B 这条边可以获得更短的到达B节点的路径，即如果 minDist[B] > minDist[A] + value，那么我们就更新 minDist[B] = minDist[A] + value ，这个过程就叫做 “松弛” 。
以上讲了这么多，其实都是围绕以下这句代码展开：
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
2
这句代码就是 Bellman_ford算法的核心操作。
以上代码也可以这么写：minDist[B] = min(minDist[A] + value, minDist[B])
如果大家看过代码随想录的动态规划章节，会发现 无论是背包问题还是子序列问题，这段代码（递推公式）出现频率非常高的。
其实 Bellman_ford算法 也是采用了动态规划的思想，即：将一个问题分解成多个决策阶段，通过状态之间的递归关系最后计算出全局最优解。
（如果理解不了动态规划的思想也无所谓，理解我上面讲的松弛操作就好）
那么为什么是 n - 1次 松弛呢？
这里要给大家模拟一遍 Bellman_ford 的算法才行，接下来我们来看看对所有边松弛 n - 1 次的操作是什么样的。
我们依然使用minDist数组来表达 起点到各个节点的最短距离，例如minDist[3] = 5 表示起点到达节点3 的最小距离为5
# 模拟过程
初始化过程。
起点为节点1， 起点到起点的距离为0，所以 minDist[1] 初始化为0
如图：
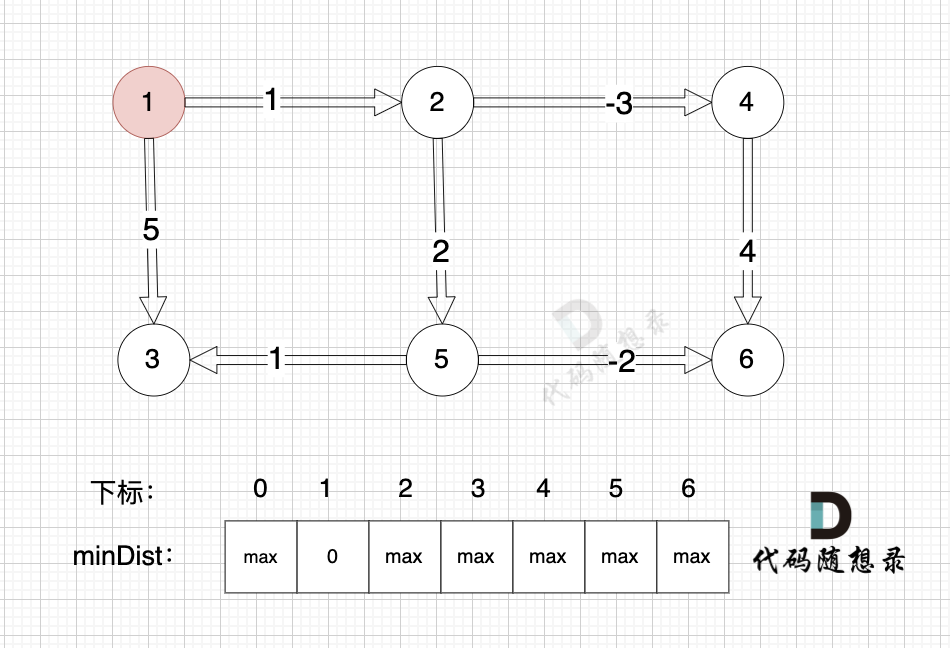
其他节点对应的minDist初始化为max，因为我们要求最小距离，那么还没有计算过的节点 默认是一个最大数，这样才能更新最小距离。
对所有边 进行第一次松弛： （什么是松弛，在上面我已经详细讲过）
以示例给出的所有边为例：
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5
2
3
4
5
6
7
接下来我们来松弛一遍所有的边。
边：节点5 -> 节点6，权值为-2 ，minDist[5] 还是默认数值max，所以不能基于 节点5 去更新节点6，如图：
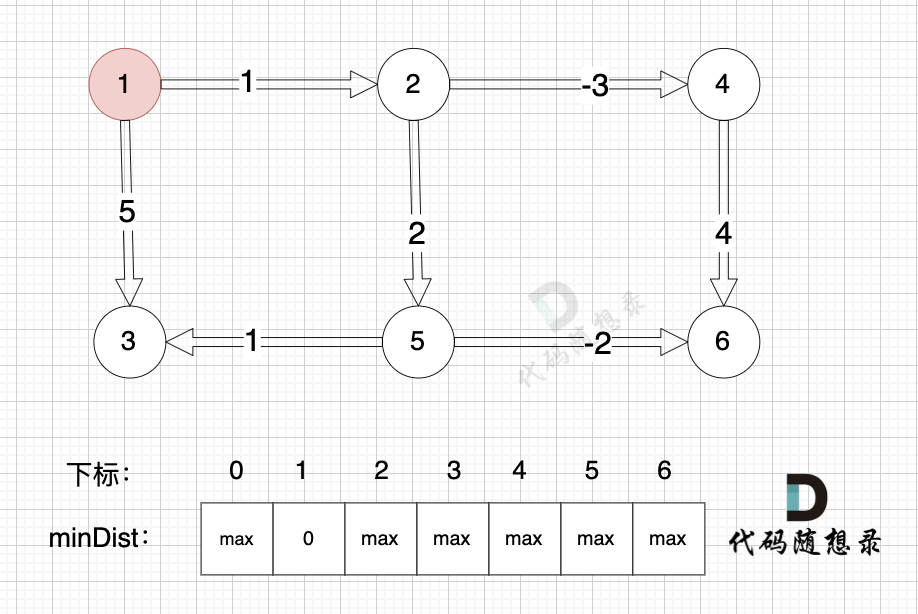
（在复习一下，minDist[5] 表示起点到节点5的最短距离）
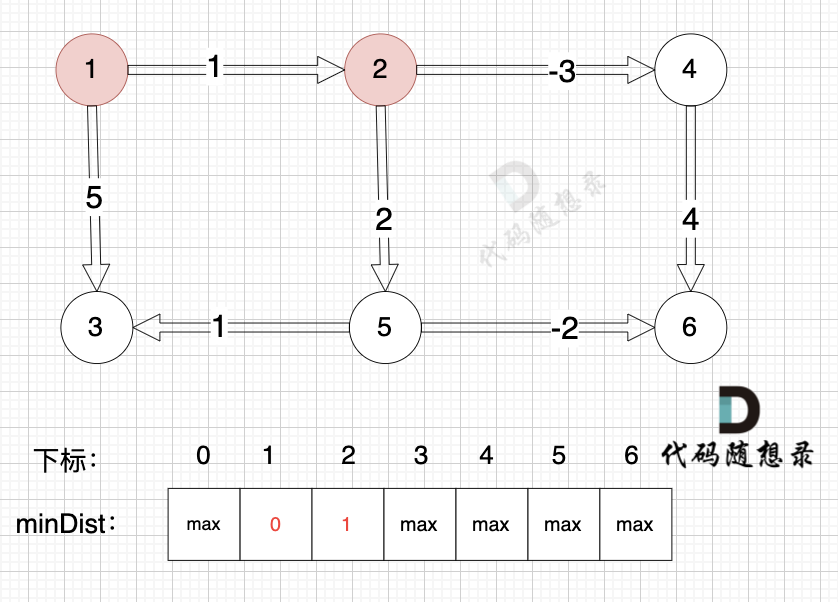
边：节点1 -> 节点2，权值为1 ，minDist[2] > minDist[1] + 1 ，更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 ，如图：
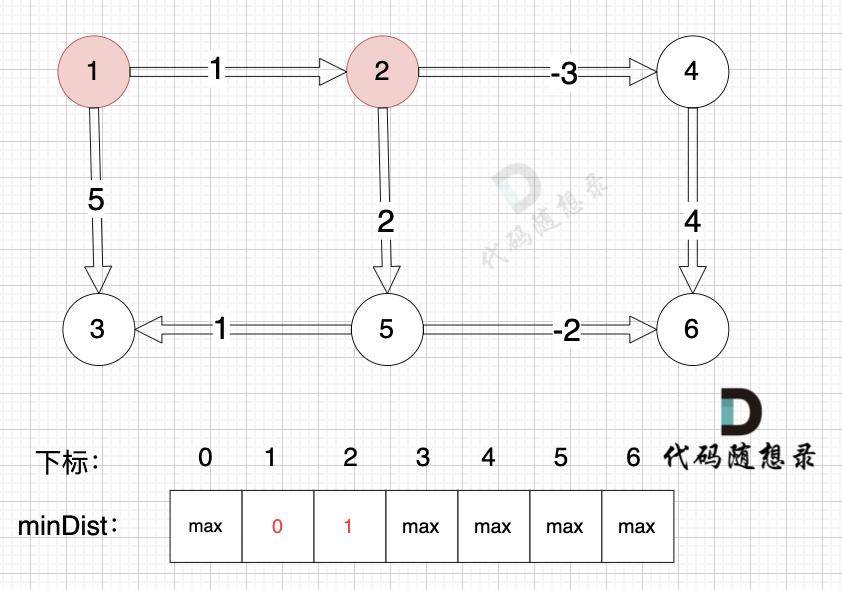
边：节点5 -> 节点3，权值为1 ，minDist[5] 还是默认数值max，所以不能基于节点5去更新节点3 如图：
边：节点2 -> 节点5，权值为2 ，minDist[5] > minDist[2] + 2 （经过上面的计算minDist[2]已经不是默认值，而是 1），更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3 ，如图：
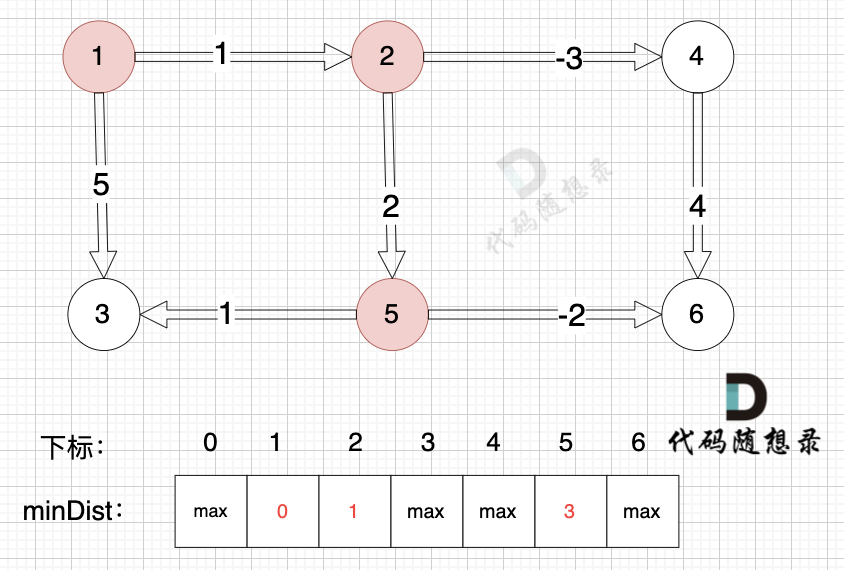
边：节点2 -> 节点4，权值为-3 ，minDist[4] > minDist[2] + (-3)，更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 ，如图：
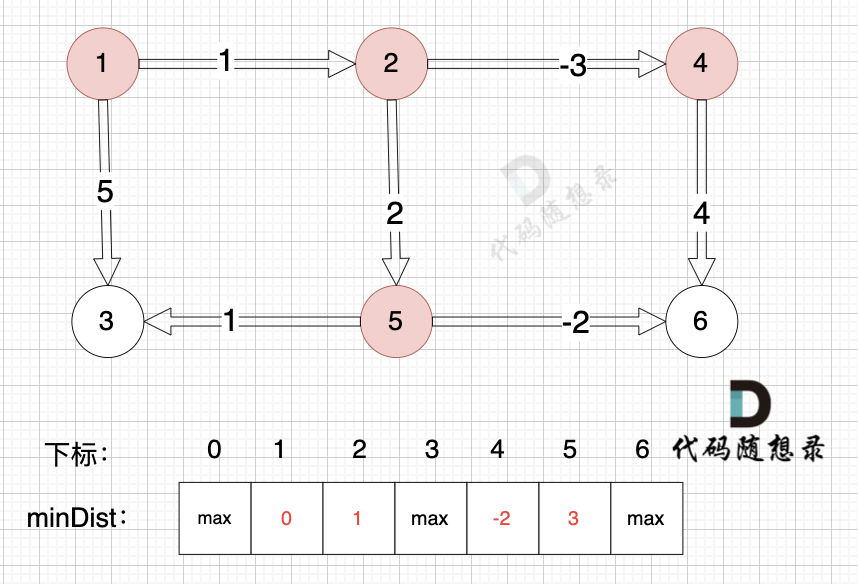
边：节点4 -> 节点6，权值为4 ，minDist[6] > minDist[4] + 4，更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2
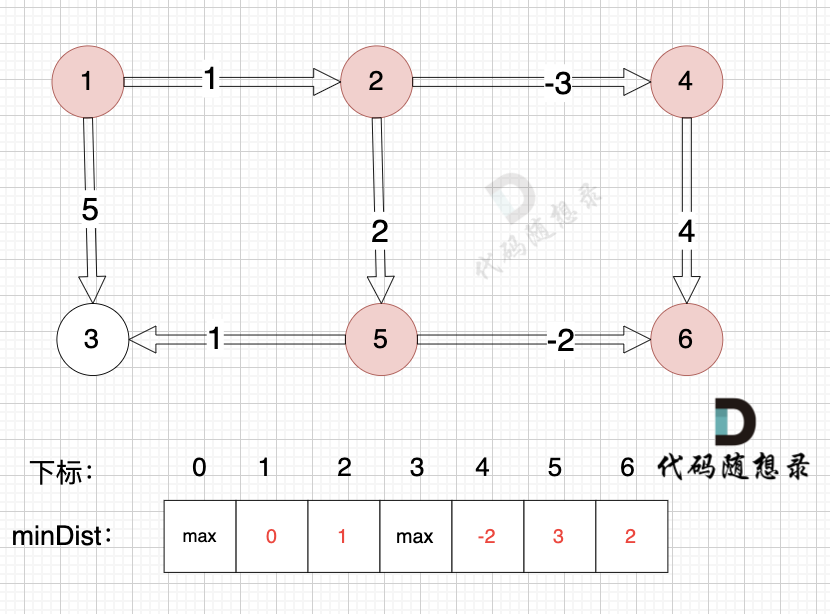
边：节点1 -> 节点3，权值为5 ，minDist[3] > minDist[1] + 5，更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5 ，如图：
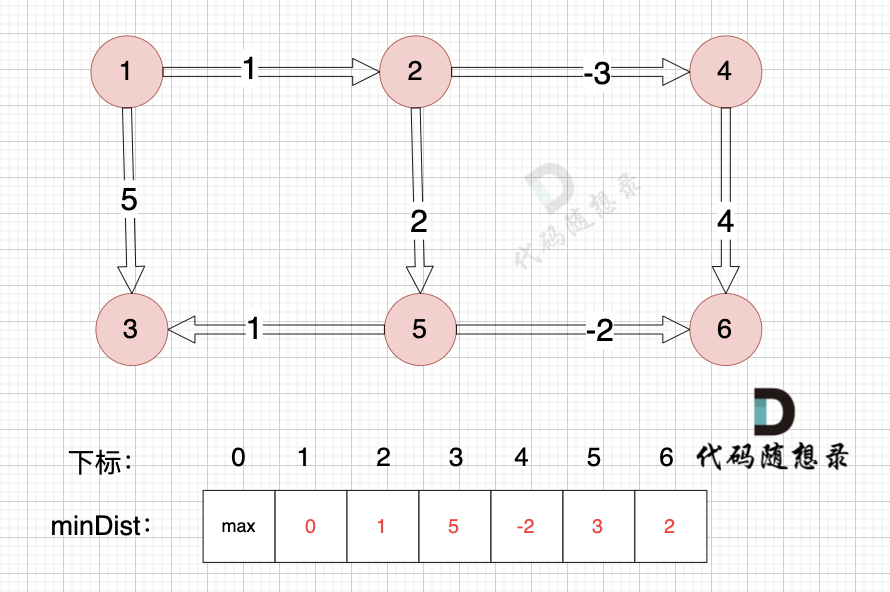
以上是对所有边进行一次松弛之后的结果。
那么需要对所有边松弛几次才能得到 起点（节点1） 到终点（节点6）的最短距离呢？
对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离。
上面的距离中，我们得到里 起点达到 与起点一条边相邻的节点2 和 节点3 的最短距离，分别是 minDist[2] 和 minDist[3]
这里有录友疑惑了 minDist[3] = 5，分明不是 起点到达 节点3 的最短距离，节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 距离才是4。
注意我上面讲的是 对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离，这里 说的是 一条边相连的节点。
与起点（节点1）一条边相邻的节点，到达节点2 最短距离是 1，到达节点3 最短距离是5。
而 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 是 与起点 三条边相连的路线了。
所以对所有边松弛一次 能得到 与起点 一条边相连的节点最短距离。
那对所有边松弛两次 可以得到与起点 两条边相连的节点的最短距离。
那对所有边松弛三次 可以得到与起点 三条边相连的节点的最短距离，这个时候，我们就能得到到达节点3真正的最短距离，也就是 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线。
那么再回归刚刚的问题，需要对所有边松弛几次才能得到 起点（节点1） 到终点（节点6）的最短距离呢？
节点数量为n，那么起点到终点，最多是 n-1 条边相连。
那么无论图是什么样的，边是什么样的顺序，我们对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
其实也同时计算出了，起点 到达 所有节点的最短距离，因为所有节点与起点连接的边数最多也就是 n-1 条边。
截止到这里，Bellman_ford 的核心算法思路，大家就了解的差不多了。
共有两个关键点。
- “松弛”究竟是个啥？
- 为什么要对所有边松弛 n - 1 次 （n为节点个数） ？
那么Bellman_ford的解题解题过程其实就是对所有边松弛 n-1 次，然后得出得到终点的最短路径。
# 代码
理解上面讲解的内容，代码就更容易写了，本题代码如下：（详细注释）
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，权值为 val
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
for (int i = 1; i < n; i++) { // 对所有边 松弛 n-1 次
for (vector<int> &side : grid) { // 每一次松弛，都是对所有边进行松弛
int from = side[0]; // 边的出发点
int to = side[1]; // 边的到达点
int price = side[2]; // 边的权值
// 松弛操作
// minDist[from] != INT_MAX 防止从未计算过的节点出发
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
minDist[to] = minDist[from] + price;
}
}
}
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
- 时间复杂度： O(N * E) , N为节点数量，E为图中边的数量
- 空间复杂度： O(N) ，即 minDist 数组所开辟的空间
关于空间复杂度，可能有录友疑惑，代码中数组grid不也开辟空间了吗？ 为什么只算minDist数组的空间呢？
grid数组是用来存图的，这是题目描述中必须要使用的空间，而不是我们算法所使用的空间。
我们在讲空间复杂度的时候，一般都是说，我们这个算法所用的空间复杂度。
# 拓展
有录友可能会想，那我 松弛 n 次，松弛 n + 1次，松弛 2 * n 次会怎么样？
其实没啥影响，结果不会变的，因为 题目中说了 “同时保证道路网络中不存在任何负权回路” 也就是图中没有 负权回路（在有向图中出现有向环 且环的总权值为负数）。
那么我们只要松弛 n - 1次 就一定能得到结果，没必要在松弛更多次了。
这里有疑惑的录友，可以加上打印 minDist数组 的日志，尝试一下，看看松弛 n 次会怎么样。
你会发现 松弛 大于 n - 1次，minDist数组 就不会变化了。
这里我给出打印日志的代码：
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，权值为 val
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
for (int i = 1; i < n; i++) { // 对所有边 松弛 n-1 次
for (vector<int> &side : grid) { // 每一次松弛，都是对所有边进行松弛
int from = side[0]; // 边的出发点
int to = side[1]; // 边的到达点
int price = side[2]; // 边的权值
// 松弛操作
// minDist[from] != INT_MAX 防止从未计算过的节点出发
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
minDist[to] = minDist[from] + price;
}
}
cout << "对所有边松弛 " << i << "次" << endl;
for (int k = 1; k <= n; k++) {
cout << minDist[k] << " ";
}
cout << endl;
}
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
通过打日志，大家发现，怎么对所有边进行第二次松弛以后结果就 不再变化了，那根本就不用松弛 n - 1 ？
这是本题的样例的特殊性， 松弛 n-1 次 是保证对任何图 都能最后求得到终点的最小距离。
如果还想不明白 我再举一个例子，用以下测试用例再跑一下。
6 5
5 6 1
4 5 1
3 4 1
2 3 1
1 2 1
2
3
4
5
6
打印结果：
对所有边松弛 1次
0 1 2147483647 2147483647 2147483647 2147483647
对所有边松弛 2次
0 1 2 2147483647 2147483647 2147483647
对所有边松弛 3次
0 1 2 3 2147483647 2147483647
对所有边松弛 4次
0 1 2 3 4 2147483647
对所有边松弛 5次
0 1 2 3 4 5
2
3
4
5
6
7
8
9
10
你会发现到 n-1 次 才打印出最后的最短路结果。
关于上面的讲解，大家一定要多写代码去实验，验证自己的想法。
至于 负权回路 ，我在下一篇会专门讲解这种情况，大家有个印象就好。
# 总结
Bellman_ford 是可以计算 负权值的单源最短路算法。
其算法核心思路是对 所有边进行 n-1 次 松弛。
弄清楚 什么是 松弛？ 为什么要 n-1 次？ 对理解Bellman_ford 非常重要。
# 其他语言版本
# Java
public class Main {
// Define an inner class Edge
static class Edge {
int from;
int to;
int val;
public Edge(int from, int to, int val) {
this.from = from;
this.to = to;
this.val = val;
}
}
public static void main(String[] args) {
// Input processing
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
List<Edge> edges = new ArrayList<>();
for (int i = 0; i < m; i++) {
int from = sc.nextInt();
int to = sc.nextInt();
int val = sc.nextInt();
edges.add(new Edge(from, to, val));
}
// Represents the minimum distance from the current node to the original node
int[] minDist = new int[n + 1];
// Initialize the minDist array
Arrays.fill(minDist, Integer.MAX_VALUE);
minDist[1] = 0;
// Starts the loop to relax all edges n - 1 times to update minDist array
for (int i = 1; i < n; i++) {
for (Edge edge : edges) {
// Updates the minDist array
if (minDist[edge.from] != Integer.MAX_VALUE && (minDist[edge.from] + edge.val) < minDist[edge.to]) {
minDist[edge.to] = minDist[edge.from] + edge.val;
}
}
}
// Outcome printing
if (minDist[n] == Integer.MAX_VALUE) {
System.out.println("unconnected");
} else {
System.out.println(minDist[n]);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# Python
def main():
n, m = map(int, input().strip().split())
edges = []
for _ in range(m):
src, dest, weight = map(int, input().strip().split())
edges.append([src, dest, weight])
minDist = [float("inf")] * (n + 1)
minDist[1] = 0 # 起点处距离为0
for i in range(1, n):
updated = False
for src, dest, weight in edges:
if minDist[src] != float("inf") and minDist[src] + weight < minDist[dest]:
minDist[dest] = minDist[src] + weight
updated = True
if not updated: # 若边不再更新，即停止回圈
break
if minDist[-1] == float("inf"): # 返还终点权重
return "unconnected"
return minDist[-1]
if __name__ == "__main__":
print(main())
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25