参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 104.建造最大岛屿
卡码网题目链接(ACM模式) (opens new window)
题目描述:
给定一个由 1(陆地)和 0(水)组成的矩阵,你最多可以将矩阵中的一格水变为一块陆地,在执行了此操作之后,矩阵中最大的岛屿面积是多少。
岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。
输入描述:
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述:
输出一个整数,表示最大的岛屿面积。
输入示例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
2
3
4
5
输出示例
6
提示信息
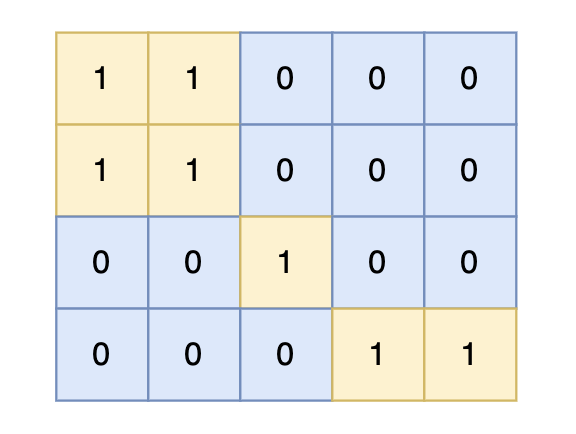
对于上面的案例,有两个位置可将 0 变成 1,使得岛屿的面积最大,即 6。
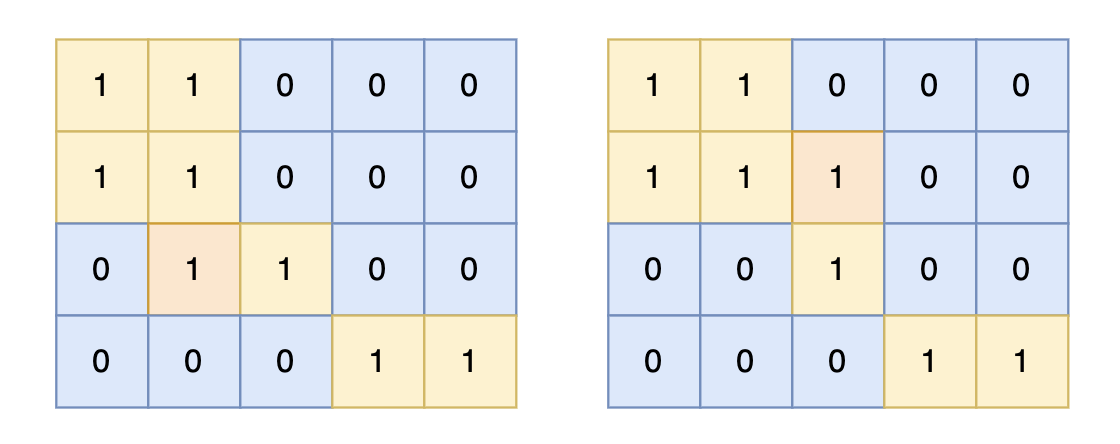
数据范围:
1 <= M, N <= 50。
# 思路
《代码随想录》算法视频公开课 (opens new window):图论:岛屿问题上难度了! |深搜优先搜索DFS | 广度优先搜索BFS | 卡码网:104.建造最大岛屿 (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
本题的一个暴力想法,应该是遍历地图尝试 将每一个 0 改成1,然后去搜索地图中的最大的岛屿面积。
计算地图的最大面积:遍历地图 + 深搜岛屿,时间复杂度为 n * n。
(其实使用深搜还是广搜都是可以的,其目的就是遍历岛屿做一个标记,相当于染色,那么使用哪个遍历方式都行,以下我用深搜来讲解)
每改变一个0的方格,都需要重新计算一个地图的最大面积,所以 整体时间复杂度为:n^4。
# 优化思路
其实每次深搜遍历计算最大岛屿面积,我们都做了很多重复的工作。
只要用一次深搜把每个岛屿的面积记录下来就好。
第一步:一次遍历地图,得出各个岛屿的面积,并做编号记录。可以使用map记录,key为岛屿编号,value为岛屿面积
第二步:再遍历地图,遍历0的方格(因为要将0变成1),并统计该1(由0变成的1)周边岛屿面积,将其相邻面积相加在一起,遍历所有 0 之后,就可以得出 选一个0变成1 之后的最大面积。
拿如下地图的岛屿情况来举例: (1为陆地)
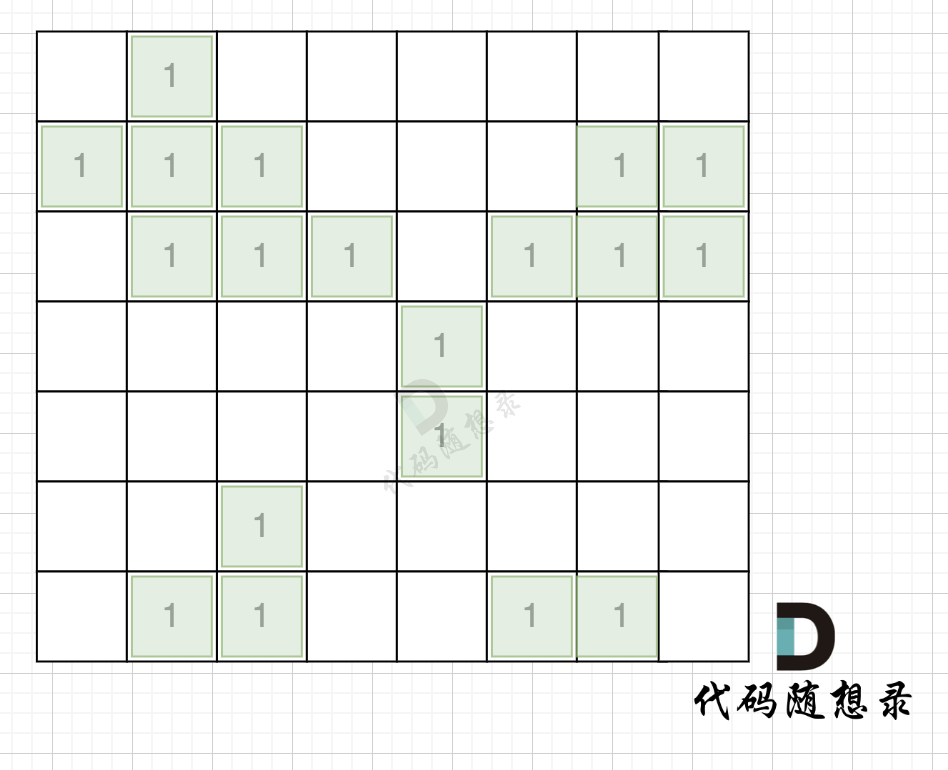
第一步,则遍历地图,并将岛屿的编号和面积都统计好,过程如图所示:
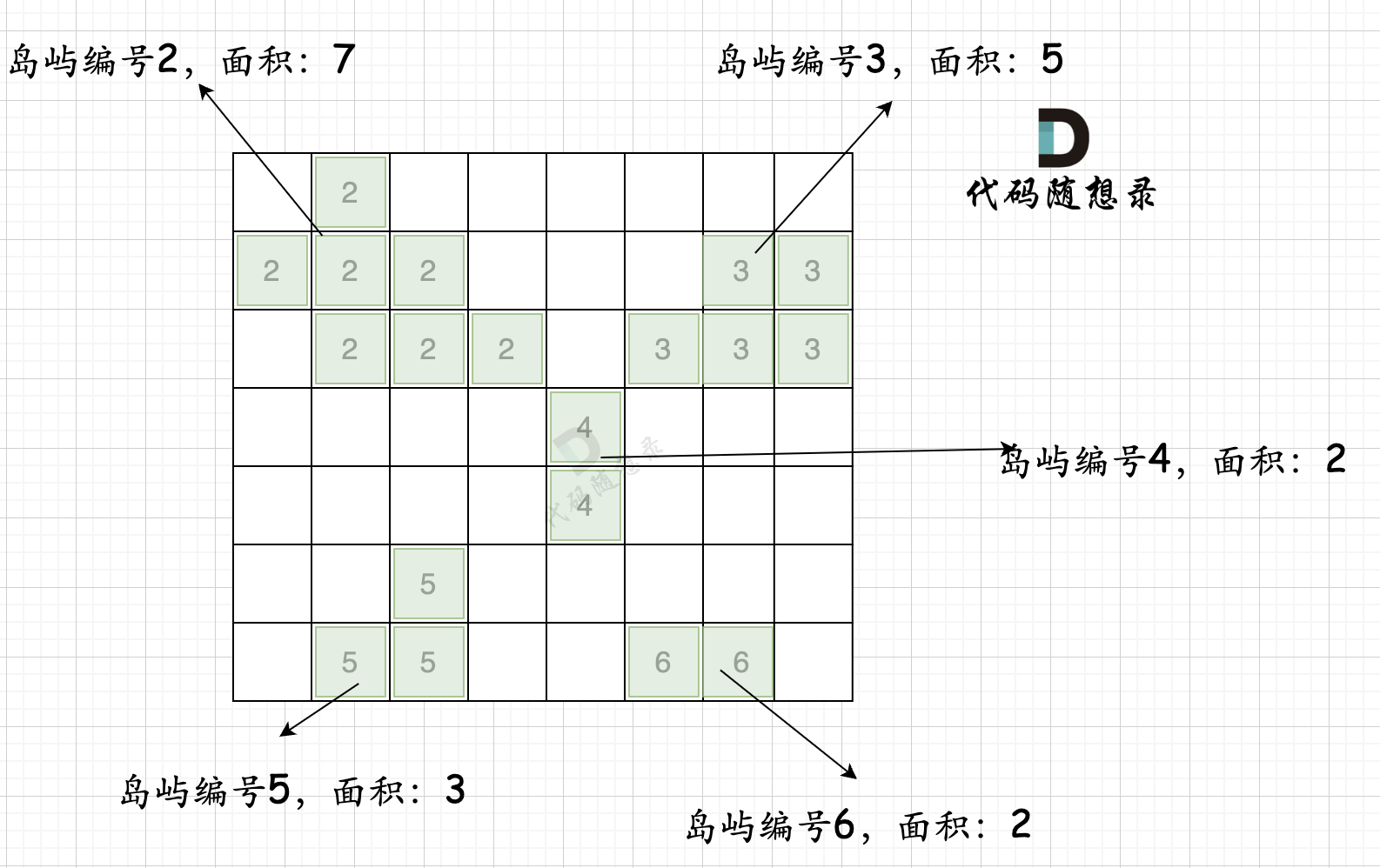
本过程代码如下:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
visited[x][y] = true; // 标记访问过
grid[x][y] = mark; // 给陆地标记新标签
count++;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
dfs(grid, visited, nextx, nexty, mark);
}
}
int largestIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false)); // 标记访问过的点
unordered_map<int ,int> gridNum;
int mark = 2; // 记录每个岛屿的编号
bool isAllGrid = true; // 标记是否整个地图都是陆地
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) isAllGrid = false;
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
gridNum[mark] = count; // 记录每一个岛屿的面积
mark++; // 记录下一个岛屿编号
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
这个过程时间复杂度 n * n 。可能有录友想:分明是两个for循环下面套这一个dfs,时间复杂度怎么回事 n * n呢?
其实大家可以仔细看一下代码,n * n这个方格地图中,每个节点我们就遍历一次,并不会重复遍历。
第二步过程如图所示:
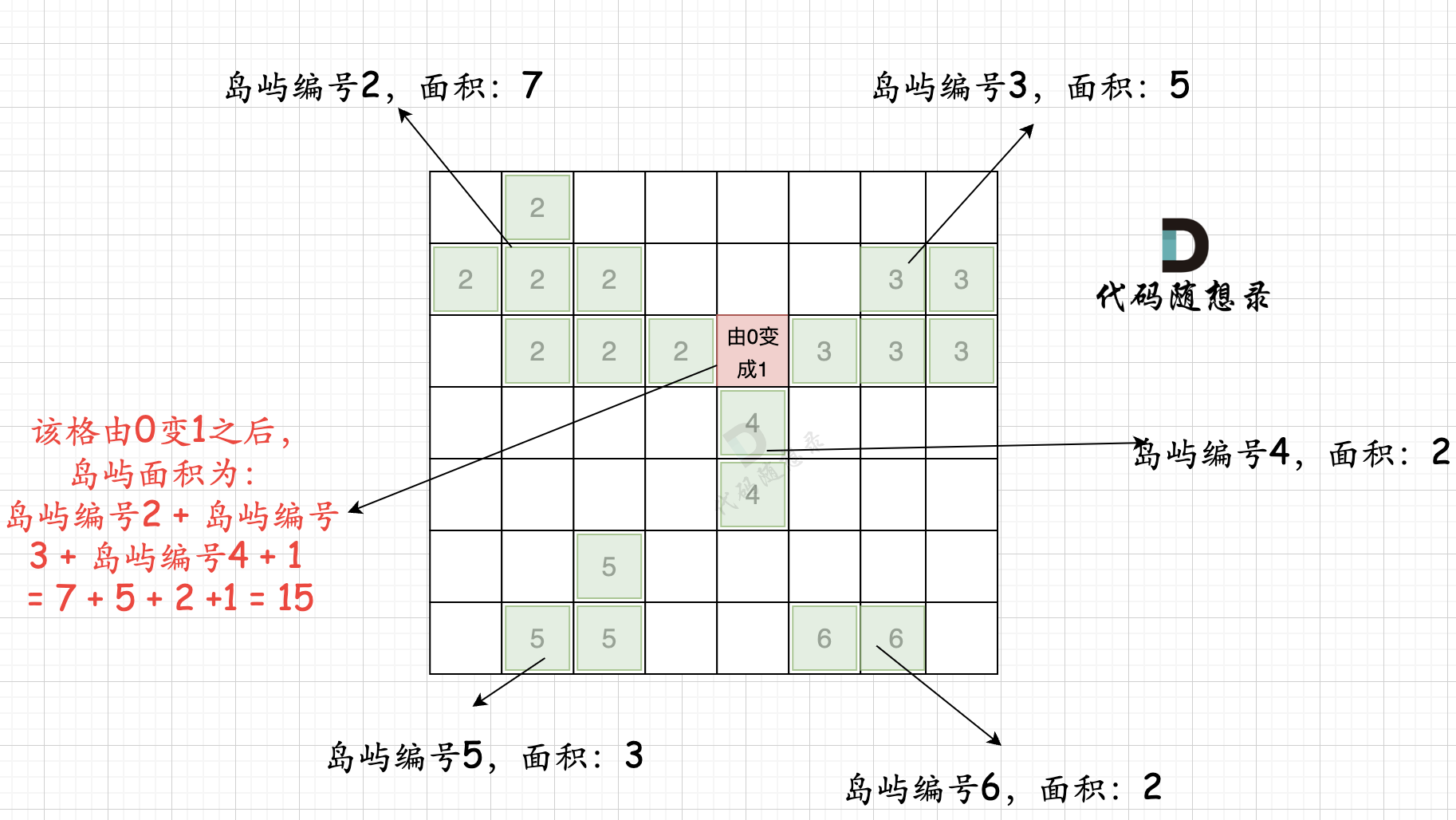
也就是遍历每一个0的方格,并统计其相邻岛屿面积,最后取一个最大值。
这个过程的时间复杂度也为 n * n。
所以整个解法的时间复杂度,为 n * n + n * n 也就是 n^2。
当然这里还有一个优化的点,就是 可以不用 visited数组,因为有mark来标记,所以遍历过的grid[i][j]是不等于1的。
代码如下:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, int x, int y, int mark) {
if (grid[x][y] != 1 || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
grid[x][y] = mark; // 给陆地标记新标签
count++;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue; // 越界了,直接跳过
dfs(grid, nextx, nexty, mark);
}
}
int main() {
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
unordered_map<int ,int> gridNum;
int mark = 2; // 记录每个岛屿的编号
bool isAllGrid = true; // 标记是否整个地图都是陆地
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) isAllGrid = false;
if (grid[i][j] == 1) {
count = 0;
dfs(grid, i, j, mark); // 将与其链接的陆地都标记上 true
gridNum[mark] = count; // 记录每一个岛屿的面积
mark++; // 记录下一个岛屿编号
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
不过为了让各个变量各司其事,代码清晰一些,完整代码还是使用visited数组来标记。
最后,整体代码如下:
#include <iostream>
#include <vector>
#include <unordered_set>
#include <unordered_map>
using namespace std;
int n, m;
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
visited[x][y] = true; // 标记访问过
grid[x][y] = mark; // 给陆地标记新标签
count++;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue; // 越界了,直接跳过
dfs(grid, visited, nextx, nexty, mark);
}
}
int main() {
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visited(n, vector<bool>(m, false)); // 标记访问过的点
unordered_map<int ,int> gridNum;
int mark = 2; // 记录每个岛屿的编号
bool isAllGrid = true; // 标记是否整个地图都是陆地
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) isAllGrid = false;
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
gridNum[mark] = count; // 记录每一个岛屿的面积
mark++; // 记录下一个岛屿编号
}
}
}
if (isAllGrid) {
cout << n * m << endl; // 如果都是陆地,返回全面积
return 0; // 结束程序
}
// 以下逻辑是根据添加陆地的位置,计算周边岛屿面积之和
int result = 0; // 记录最后结果
unordered_set<int> visitedGrid; // 标记访问过的岛屿
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
count = 1; // 记录连接之后的岛屿数量
visitedGrid.clear(); // 每次使用时,清空
if (grid[i][j] == 0) {
for (int k = 0; k < 4; k++) {
int neari = i + dir[k][1]; // 计算相邻坐标
int nearj = j + dir[k][0];
if (neari < 0 || neari >= n || nearj < 0 || nearj >= m) continue;
if (visitedGrid.count(grid[neari][nearj])) continue; // 添加过的岛屿不要重复添加
// 把相邻四面的岛屿数量加起来
count += gridNum[grid[neari][nearj]];
visitedGrid.insert(grid[neari][nearj]); // 标记该岛屿已经添加过
}
}
result = max(result, count);
}
}
cout << result << endl;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
# 其他语言版本
# Java
public class Main {
// 该方法采用 DFS
// 定义全局变量
// 记录每次每个岛屿的面积
static int count;
// 对每个岛屿进行标记
static int mark;
// 定义二维数组表示四个方位
static int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
// DFS 进行搜索,将每个岛屿标记为不同的数字
public static void dfs(int[][] grid, int x, int y, boolean[][] visited) {
// 当遇到边界,直接return
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length) return;
// 遇到已经访问过的或者遇到海水,直接返回
if (visited[x][y] || grid[x][y] == 0) return;
visited[x][y] = true;
count++;
grid[x][y] = mark;
// 继续向下层搜索
dfs(grid, x, y + 1, visited);
dfs(grid, x, y - 1, visited);
dfs(grid, x + 1, y, visited);
dfs(grid, x - 1, y, visited);
}
public static void main (String[] args) {
// 接收输入
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
int[][] grid = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
grid[i][j] = sc.nextInt();
}
}
// 初始化mark变量,从2开始(区别于0水,1岛屿)
mark = 2;
// 定义二位boolean数组记录该位置是否被访问
boolean[][] visited = new boolean[m][n];
// 定义一个HashMap,记录某片岛屿的标记号和面积
HashMap<Integer, Integer> getSize = new HashMap<>();
// 定义一个HashSet,用来判断某一位置水四周是否存在不同标记编号的岛屿
HashSet<Integer> set = new HashSet<>();
// 定义一个boolean变量,看看DFS之后,是否全是岛屿
boolean isAllIsland = true;
// 遍历二维数组进行DFS搜索,标记每片岛屿的编号,记录对应的面积
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 0) isAllIsland = false;
if (grid[i][j] == 1) {
count = 0;
dfs(grid, i, j, visited);
getSize.put(mark, count);
mark++;
}
}
}
int result = 0;
if (isAllIsland) result = m * n;
// 对标记完的grid继续遍历,判断每个水位置四周是否有岛屿,并记录下四周不同相邻岛屿面积之和
// 每次计算完一个水位置周围可能存在的岛屿面积之和,更新下result变量
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 0) {
set.clear();
// 当前水位置变更为岛屿,所以初始化为1
int curSize = 1;
for (int[] dir : dirs) {
int curRow = i + dir[0];
int curCol = j + dir[1];
if (curRow < 0 || curRow >= m || curCol < 0 || curCol >= n) continue;
int curMark = grid[curRow][curCol];
// 如果当前相邻的岛屿已经遍历过或者HashMap中不存在这个编号,继续搜索
if (set.contains(curMark) || !getSize.containsKey(curMark)) continue;
set.add(curMark);
curSize += getSize.get(curMark);
}
result = Math.max(result, curSize);
}
}
}
// 打印结果
System.out.println(result);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
# Python
# BFS
from typing import List
from collections import defaultdict
class Solution:
def __init__(self):
self.direction = [(1,0),(-1,0),(0,1),(0,-1)]
self.res = 0
self.count = 0
self.idx = 1
self.count_area = defaultdict(int)
def max_area_island(self, grid: List[List[int]]) -> int:
if not grid or len(grid) == 0 or len(grid[0]) == 0:
return 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
self.count = 0
self.idx += 1
self.dfs(grid,i,j)
# print(grid)
self.check_area(grid)
# print(self.count_area)
if self.check_largest_connect_island(grid=grid):
return self.res + 1
return max(self.count_area.values())
def dfs(self,grid,row,col):
grid[row][col] = self.idx
self.count += 1
for dr,dc in self.direction:
_row = dr + row
_col = dc + col
if 0<=_row<len(grid) and 0<=_col<len(grid[0]) and grid[_row][_col] == 1:
self.dfs(grid,_row,_col)
return
def check_area(self,grid):
m, n = len(grid), len(grid[0])
for row in range(m):
for col in range(n):
self.count_area[grid[row][col]] = self.count_area.get(grid[row][col],0) + 1
return
def check_largest_connect_island(self,grid):
m, n = len(grid), len(grid[0])
has_connect = False
for row in range(m):
for col in range(n):
if grid[row][col] == 0:
has_connect = True
area = 0
visited = set()
for dr, dc in self.direction:
_row = row + dr
_col = col + dc
if 0<=_row<len(grid) and 0<=_col<len(grid[0]) and grid[_row][_col] != 0 and grid[_row][_col] not in visited:
visited.add(grid[_row][_col])
area += self.count_area[grid[_row][_col]]
self.res = max(self.res, area)
return has_connect
def main():
m, n = map(int, input().split())
grid = []
for i in range(m):
grid.append(list(map(int,input().split())))
sol = Solution()
print(sol.max_area_island(grid))
if __name__ == '__main__':
main()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import collections
directions = [[-1, 0], [0, 1], [0, -1], [1, 0]]
area = 0
def dfs(i, j, grid, visited, num):
global area
if visited[i][j]:
return
visited[i][j] = True
grid[i][j] = num # 标记岛屿号码
area += 1
for x, y in directions:
new_x = i + x
new_y = j + y
if (
0 <= new_x < len(grid)
and 0 <= new_y < len(grid[0])
and grid[new_x][new_y] == "1"
):
dfs(new_x, new_y, grid, visited, num)
def main():
global area
N, M = map(int, input().strip().split())
grid = []
for i in range(N):
grid.append(input().strip().split())
visited = [[False] * M for _ in range(N)]
rec = collections.defaultdict(int)
cnt = 2
for i in range(N):
for j in range(M):
if grid[i][j] == "1":
area = 0
dfs(i, j, grid, visited, cnt)
rec[cnt] = area # 纪录岛屿面积
cnt += 1
res = 0
for i in range(N):
for j in range(M):
if grid[i][j] == "0":
max_island = 1 # 将水变为陆地,故从1开始计数
v = set()
for x, y in directions:
new_x = i + x
new_y = j + y
if (
0 <= new_x < len(grid)
and 0 <= new_y < len(grid[0])
and grid[new_x][new_y] != "0"
and grid[new_x][new_y] not in v # 岛屿不可重复
):
max_island += rec[grid[new_x][new_y]]
v.add(grid[new_x][new_y])
res = max(res, max_island)
if res == 0:
return max(rec.values()) # 无水的情况
return res
if __name__ == "__main__":
print(main())
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# Go
# Rust
# JavaScript
const r1 = require('readline').createInterface({ input: process.stdin });
// 创建readline接口
let iter = r1[Symbol.asyncIterator]();
// 创建异步迭代器
const readline = async () => (await iter.next()).value;
let graph // 地图
let N, M // 地图大小
let visited // 访问过的节点, 标记岛屿
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
let count = 0 // 统计岛屿面积
let areaMap = new Map() // 存储岛屿面积
// 读取输入,初始化地图
const initGraph = async () => {
let line = await readline();
[N, M] = line.split(' ').map(Number);
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
visited = new Array(N).fill(0).map(() => new Array(M).fill(0))
for (let i = 0; i < N; i++) {
line = await readline()
line = line.split(' ').map(Number)
for (let j = 0; j < M; j++) {
graph[i][j] = line[j]
}
}
}
/**
* @description: 从(x,y)开始深度优先遍历地图
* @param {*} graph 地图
* @param {*} visited 可访问节点
* @param {*} x 开始搜索节点的下标
* @param {*} y 开始搜索节点的下标
* @param {*} mark 当前岛屿的标记
* @return {*}
*/
const dfs = (graph, visited, x, y, mark) => {
if (visited[x][y] != 0) return
visited[x][y] = mark
count++
for (let i = 0; i < 4; i++) {
let nextx = x + dir[i][0]
let nexty = y + dir[i][1]
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
// 已访问过, 或者是海洋, 跳过
if (visited[nextx][nexty] != 0 || graph[nextx][nexty] == 0) continue
dfs(graph, visited, nextx, nexty, mark)
}
}
(async function () {
// 读取输入,初始化地图
await initGraph()
let isAllLand = true //标记整个地图都是陆地
let mark = 2 // 标记岛屿
for (let i = 0; i < N; i++) {
for (let j = 0; j < M; j++) {
if (graph[i][j] == 0 && isAllLand) isAllLand = false
if (graph[i][j] === 1 && visited[i][j] === 0) {
count = 0
dfs(graph, visited, i, j, mark)
areaMap.set(mark, count)
mark++
}
}
}
// 如果全是陆地, 直接返回面积
if (isAllLand) {
console.log(N * M);
return
}
let result = 0 // 记录最后结果
let visitedIsland = new Map() //标记访问过的岛屿, 因为海洋四周可能是同一个岛屿, 需要标记避免重复统计面积
for (let i = 0; i < N; i++) {
for (let j = 0; j < M; j++) {
if (visited[i][j] === 0) {
count = 1 // 记录连接之后的岛屿数量
visitedIsland.clear() // 每次使用时,清空
// 计算海洋周围岛屿面积
for (let m = 0; m < 4; m++) {
const nextx = i + dir[m][0]
const nexty = j + dir[m][1]
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
const island = visited[nextx][nexty]
if (island == 0 || visitedIsland.get(island)) continue// 四周是海洋或者访问过的陆地 跳过
// 标记为访问, 计算面积
visitedIsland.set(island, true)
count += areaMap.get(visited[nextx][nexty])
}
result = Math.max(result, count)
}
}
}
console.log(result);
})()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112

评论
验证登录状态...