代码随想录

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

# 110. 字符串接龙

卡码网题目链接（ACM模式） (opens new window)

题目描述

字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列：

  1. 序列中第一个字符串是 beginStr。

  2. 序列中最后一个字符串是 endStr。

  3. 每次转换只能改变一个字符。

  4. 转换过程中的中间字符串必须是字典 strList 中的字符串。

给你两个字符串 beginStr 和 endStr 和一个字典 strList，找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列，返回 0。

输入描述

第一行包含一个整数 N，表示字典 strList 中的字符串数量。 第二行包含两个字符串，用空格隔开，分别代表 beginStr 和 endStr。 后续 N 行，每行一个字符串，代表 strList 中的字符串。

输出描述

输出一个整数，代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列，则输出 0。

输入示例

6
abc def
efc
dbc
ebc
dec
dfc
yhn
1
2
3
4
5
6
7
8

输出示例

4

提示信息

从 startStr 到 endStr，在 strList 中最短的路径为 abc -> dbc -> dec -> def，所以输出结果为 4

数据范围：

2 <= N <= 500

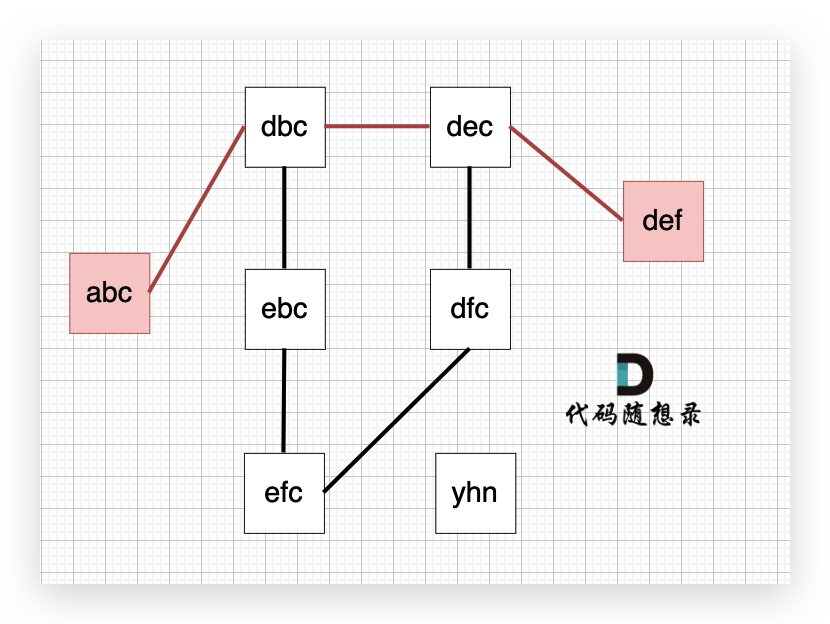
# 思路

以示例1为例，从这个图中可以看出 abc 到 def的路线 不止一条，但最短的一条路径上是4个节点。

本题只需要求出最短路径的长度就可以了，不用找出具体路径。

所以这道题要解决两个问题：

  • 图中的线是如何连在一起的
  • 起点和终点的最短路径长度

首先题目中并没有给出点与点之间的连线，而是要我们自己去连，条件是字符只能差一个。

所以判断点与点之间的关系，需要判断是不是差一个字符，如果差一个字符，那就是有链接。

然后就是求起点和终点的最短路径长度，这里无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。

本题如果用深搜，会比较麻烦，要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点，一定是最短路。

另外需要有一个注意点：

  • 本题是一个无向图，需要用标记位，标记着节点是否走过，否则就会死循环！
  • 使用set来检查字符串是否出现在字符串集合里更快一些

C++代码如下：（详细注释）

#include <iostream>
#include <vector>
#include <string>
#include <unordered_set>
#include <unordered_map>
#include <queue>
using namespace std;
int main() {
    string beginStr, endStr, str;
    int n;
    cin >> n;
    unordered_set<string> strSet;
    cin >> beginStr >> endStr;
    for (int i = 0; i < n; i++) {
        cin >> str;
        strSet.insert(str);
    }

    // 记录strSet里的字符串是否被访问过，同时记录路径长度
    unordered_map<string, int> visitMap; // <记录的字符串，路径长度>

    // 初始化队列
    queue<string> que;
    que.push(beginStr);

    // 初始化visitMap
    visitMap.insert(pair<string, int>(beginStr, 1));

    while(!que.empty()) {
        string word = que.front();
        que.pop();
        int path = visitMap[word]; // 这个字符串在路径中的长度

        // 开始在这个str中，挨个字符去替换
        for (int i = 0; i < word.size(); i++) {
            string newWord = word; // 用一个新字符串替换str，因为每次要置换一个字符

            // 遍历26的字母
            for (int j = 0 ; j < 26; j++) {
                newWord[i] = j + 'a';
                if (newWord == endStr) { // 发现替换字母后，字符串与终点字符串相同
                    cout <<  path + 1 << endl; // 找到了路径 
                    return 0;
                }
                // 字符串集合里出现了newWord，并且newWord没有被访问过
                if (strSet.find(newWord) != strSet.end()
                        && visitMap.find(newWord) == visitMap.end()) {
                    // 添加访问信息，并将新字符串放到队列中
                    visitMap.insert(pair<string, int>(newWord, path + 1));
                    que.push(newWord);
                }
            }
        }
    }

    // 没找到输出0
    cout << 0 << endl;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

当然本题也可以用双向BFS，就是从头尾两端进行搜索，大家感兴趣，可以自己去实现，这里就不再做详细讲解了。

# 其他语言版本

# Java

public class Main {
    // BFS方法
    public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 使用set作为查询容器，效率更高
        HashSet<String> set = new HashSet<>(wordList);
        
        // 声明一个queue存储每次变更一个字符得到的且存在于容器中的新字符串
        Queue<String> queue = new LinkedList<>();
        
        // 声明一个hashMap存储遍历到的字符串以及所走过的路径path
        HashMap<String, Integer> visitMap = new HashMap<>();
        queue.offer(beginWord);
        visitMap.put(beginWord, 1);
        
        while (!queue.isEmpty()) {
            String curWord = queue.poll();
            int path = visitMap.get(curWord);

            for (int i = 0; i < curWord.length(); i++) {
                char[] ch = curWord.toCharArray();
                // 每个位置尝试26个字母
                for (char k = 'a'; k <= 'z'; k++) {
                    ch[i] = k;

                    String newWord = new String(ch);
                    if (newWord.equals(endWord)) return path + 1;
                    
                    // 如果这个新字符串存在于容器且之前未被访问到
                    if (set.contains(newWord) && !visitMap.containsKey(newWord)) {
                        visitMap.put(newWord, path + 1);
                        queue.offer(newWord);
                    }
                }
            }
        }

        return 0;
    }
    
    public static void main (String[] args) {
        /* code */
        // 接收输入
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        sc.nextLine();
        String[] strs = sc.nextLine().split(" ");
        
        List<String> wordList = new ArrayList<>();
        for (int i = 0; i < N; i++) {
            wordList.add(sc.nextLine());
        }
        
        // wordList.add(strs[1]);
        
        // 打印结果
        int result = ladderLength(strs[0], strs[1], wordList);
        System.out.println(result);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

# Python

def judge(s1,s2):
    count=0
    for i in range(len(s1)):
        if s1[i]!=s2[i]:
            count+=1
    return count==1

if __name__=='__main__':
    n=int(input())
    beginstr,endstr=map(str,input().split())
    if beginstr==endstr:
        print(0)
        exit()
    strlist=[]
    for i in range(n):
        strlist.append(input())
    
    # use bfs
    visit=[False for i in range(n)]
    queue=[[beginstr,1]]
    while queue:
        str,step=queue.pop(0)
        if judge(str,endstr):
            print(step+1)
            exit()
        for i in range(n):
            if visit[i]==False and judge(strlist[i],str):
                visit[i]=True
                queue.append([strlist[i],step+1])
    print(0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# Go

# Rust

# Javascript

const r1 = require('readline').createInterface({ input: process.stdin });
// 创建readline接口
let iter = r1[Symbol.asyncIterator]();
// 创建异步迭代器
const readline = async () => (await iter.next()).value;

let N //输入字符串个数
let beginStr //开始字符串
let endStr //结束字符串
let strSet = new Set() //字符串集合
let visitedMap = new Map() //访问过的字符串

// 读取输入，初始化地图
const init = async () => {
  let line = await readline();
  line = line.trim()
  N = Number(line);

  line = await readline();
  line = line.trim().split(' ')
  beginStr = line[0]
  endStr = line[1]

  for (let i = 0; i < N; i++) {
    line = await readline()
    line = line.trim()
    strSet.add(line.trim())
  }
}

(async function () {

  // 读取输入，初始化数据
  await init()

  // 初始化队列
  let queue = []
  queue.push(beginStr)

  // 初始化visitMap
  visitedMap.set(beginStr, 1)

  while (queue.length) {
    let word = queue.shift()
    let path = visitedMap.get(word)

    // 遍历26个字母
    for (let i = 0; i < word.length; i++) {
      let newWord = word.split('') // 用一个新字符串替换str，因为每次要置换一个字符
      for (let j = 0; j < 26; j++) {
        newWord[i] = String.fromCharCode('a'.charCodeAt() + j)
        // 发现替换字母后，字符串与终点字符串相同
        if (newWord.join('') === endStr) {
          console.log(path + 1);
          return 0;   // 找到了路径 
        }

        // 字符串集合里出现了newWord，并且newWord没有被访问过
        if (strSet.has(newWord.join('')) && !visitedMap.has(newWord.join(''))) {
          // 添加访问信息，并将新字符串放到队列中
          queue.push(newWord.join(''))
          visitedMap.set(newWord.join(''), path + 1)
        }
      }
    }
  }

  console.log(0);
})()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

# TypeScript

# PhP

# Swift

# Scala

# C#

# Dart

# C

上次更新：: 8/29/2024, 9:07:04 PM

← 13. 有向图的完全可达性 →

@2021-2024 代码随想录 版权所有 粤ICP备19156078号