# 108. 冗余连接
卡码网题目链接(ACM模式) (opens new window)
题目描述
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图(其实就是一个线形图),如图:
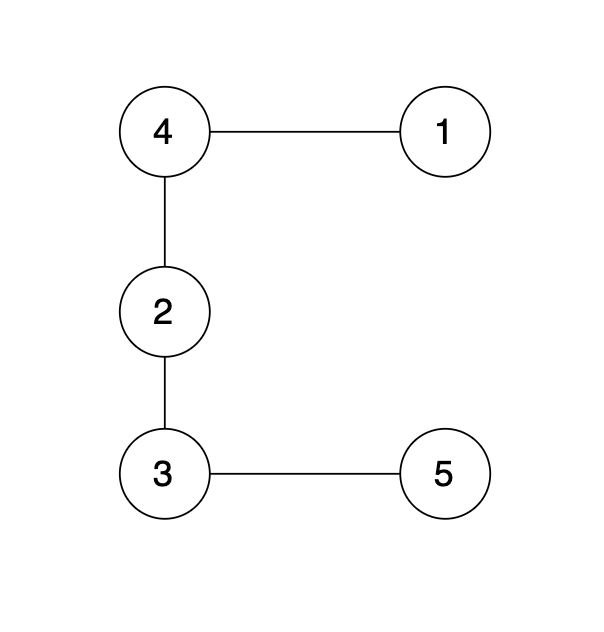
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图
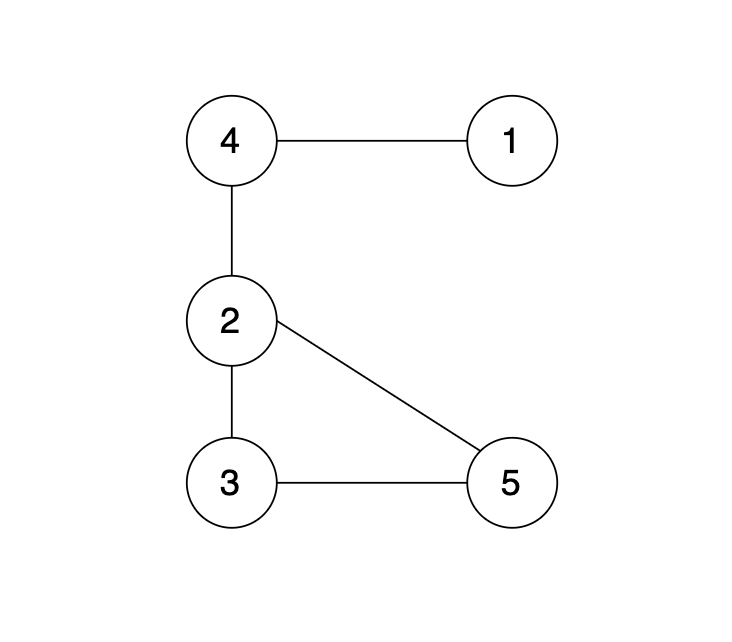
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
输入描述
第一行包含一个整数 N,表示图的节点个数和边的个数。
后续 N 行,每行包含两个整数 s 和 t,表示图中 s 和 t 之间有一条边。
输出描述
输出一条可以删除的边。如果有多个答案,请删除标准输入中最后出现的那条边。
输入示例
3
1 2
2 3
1 3
2
3
4
输出示例
1 3
提示信息
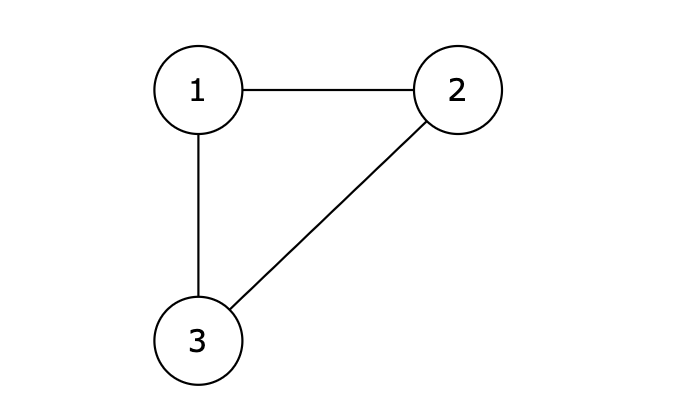
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输入里最后出现的那条边,所以输出结果为 1 3
数据范围:
1 <= N <= 1000.
# 思路
《代码随想录》算法视频公开课 (opens new window):图论:并查集有点不简单了。。 (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
这道题目也是并查集基础题目。
这里我依然降调一下,并查集可以解决什么问题:两个节点是否在一个集合,也可以将两个节点添加到一个集合中。
如果还不了解并查集,可以看这里:并查集理论基础
我们再来看一下这道题目。
题目说是无向图,返回一条可以删去的边,使得结果图是一个有着N个节点的树(即:只有一个根节点)。
如果有多个答案,则返回二维数组中最后出现的边。
那么我们就可以从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
如图所示,节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
如图所示:
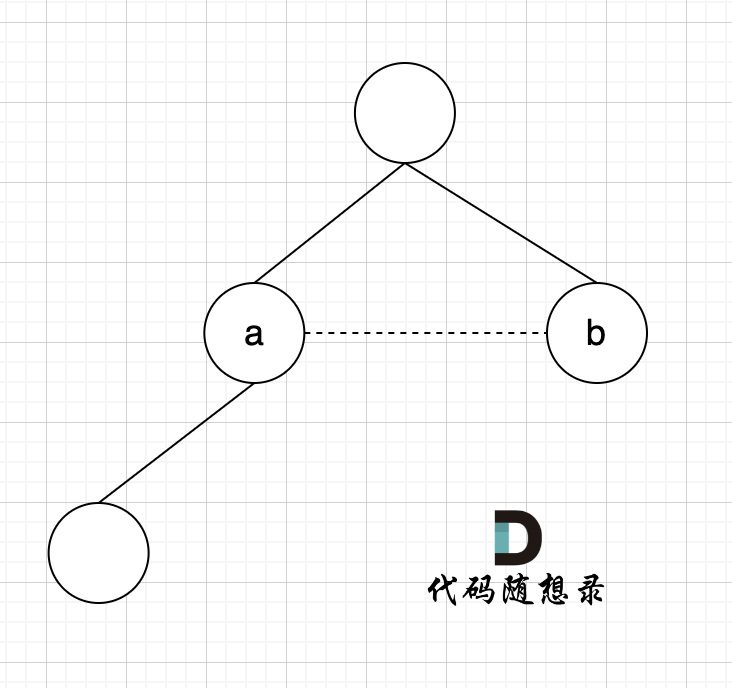
已经判断 节点A 和 节点B 在在同一个集合(同一个根),如果将 节点A 和 节点B 连在一起就一定会出现环。
这个思路清晰之后,代码就很好写了。
并查集C++代码如下:
#include <iostream>
#include <vector>
using namespace std;
int n; // 节点数量
vector<int> father(1001, 0); // 按照节点大小范围定义数组
// 并查集初始化
void init() {
for (int i = 0; i <= n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}
int main() {
int s, t;
cin >> n;
init();
for (int i = 0; i < n; i++) {
cin >> s >> t;
if (isSame(s, t)) {
cout << s << " " << t << endl;
return 0;
} else {
join(s, t);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
可以看出,主函数的代码很少,就判断一下边的两个节点在不在同一个集合就可以了。
# 拓展
题目要求 “请删除标准输入中最后出现的那条边” ,不少录友疑惑,这代码分明是遇到在同一个根的两个节点立刻就返回了,怎么就求出 最后出现的那条边 了呢。
有这种疑惑的录友是 认为发现一条冗余边后,后面还可能会有一条冗余边。
其实并不会。
题目是在 树的基础上 添加一条边,所以冗余边仅仅是一条。
到这一条可能靠前出现,可能靠后出现。
例如,题目输入示例:
输入示例
3
1 2
2 3
1 3
2
3
4
图:

输出示例
1 3
当我们从前向后遍历,优先让前面的边连上,最后判断冗余边就是 1 3。
如果我们从后向前便利,优先让后面的边连上,最后判断的冗余边就是 1 2。
题目要求“请删除标准输入中最后出现的那条边”,所以 1 3 这条边才是我们要求的。
# 其他语言版本
# Java
import java.util.Scanner;
public class Main {
private static int[] father;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int pointNum = scanner.nextInt();
father = new int[pointNum + 1];
init();
for (int i = 0; i < pointNum; i++) {
join(scanner.nextInt(), scanner.nextInt());
}
}
/**
* 并查集初始化
*/
private static void init() {
for (int i = 1; i < father.length; i++) {
// 让每个元素指向自己
father[i] = i;
}
}
/**
* 并查集寻根
*
* @param u
* @return
*/
private static int find(int u) {
// 判断 u 是否等于自己,如果是的话,直接返回自己
// 如果不等于自己,就寻找根,寻找的时候,反复进行路径压缩
return u == father[u] ? u : (father[u] = find(father[u]));
}
/**
* 判断 u 和 v 是否同根
*
* @param u
* @param v
* @return
*/
private static boolean isSame(int u, int v) {
return find(u) == find(v);
}
/**
* 添加 边 到并查集,v 指向 u
*
* @param u
* @param v
*/
private static void join(int u, int v) {
// --if-- 如果两个点已经同根,说明他们的信息已经存储到并查集中了,直接返回即可
// 寻找u的根
int uRoot = find(u);
// 寻找v的根
int vRoot = find(v);
if (uRoot == vRoot) {
// --if-- 如果u,v的根相同,说明两者已经连接了,直接输出
System.out.println(u + " " + v);
return;
}
// --if-- 将信息添加到并查集
father[vRoot] = uRoot;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# Python
father = list()
def find(u):
if u == father[u]:
return u
else:
father[u] = find(father[u])
return father[u]
def is_same(u, v):
u = find(u)
v = find(v)
return u == v
def join(u, v):
u = find(u)
v = find(v)
if u != v:
father[u] = v
if __name__ == "__main__":
# 輸入
n = int(input())
for i in range(n + 1):
father.append(i)
# 尋找冗余邊
result = None
for i in range(n):
s, t = map(int, input().split())
if is_same(s, t):
result = str(s) + ' ' + str(t)
else:
join(s, t)
# 輸出
print(result)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Go
# Rust
# JavaScript
const r1 = require('readline').createInterface({ input: process.stdin });
// 创建readline接口
let iter = r1[Symbol.asyncIterator]();
// 创建异步迭代器
const readline = async () => (await iter.next()).value;
let N // 节点数和边数
let father = [] // 并查集
// 并查集初始化
const init = () => {
for (let i = 1; i <= N; i++) father[i] = i;
}
// 并查集里寻根的过程
const find = (u) => {
return u == father[u] ? u : father[u] = find(father[u])
}
// 将v->u 这条边加入并查集
const join = (u, v) => {
u = find(u)
v = find(v)
if (u == v) return // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u
}
// 判断 u 和 v是否找到同一个根
const isSame = (u, v) => {
u = find(u)
v = find(v)
return u == v
}
(async function () {
// 读取第一行输入
let line = await readline();
N = Number(line);
// 初始化并查集
father = new Array(N)
init()
// 读取边信息, 加入并查集
for (let i = 0; i < N; i++) {
line = await readline()
line = line.split(' ').map(Number)
if (!isSame(line[0], line[1])) {
join(line[0], line[1])
}else{
console.log(line[0], line[1]);
break
}
}
})()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
