参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# Floyd 算法精讲
卡码网:97. 小明逛公园 (opens new window)
【题目描述】
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
【输入描述】
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
【输出描述】
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
【输入示例】
7 3 1 2 4 2 5 6 3 6 8 2 1 2 2 3
【输出示例】
4 -1
【提示信息】
从 1 到 2 的路径长度为 4,2 到 3 之间并没有道路。
1 <= N, M, Q <= 1000.
# 思路
本题是经典的多源最短路问题。
在这之前我们讲解过,dijkstra朴素版、dijkstra堆优化、Bellman算法、Bellman队列优化(SPFA) 都是单源最短路,即只能有一个起点。
而本题是多源最短路,即 求多个起点到多个终点的多条最短路径。
通过本题,我们来系统讲解一个新的最短路算法-Floyd 算法。
Floyd 算法对边的权值正负没有要求,都可以处理。
Floyd算法核心思想是动态规划。
例如我们再求节点1 到 节点9 的最短距离,用二维数组来表示即:grid[1][9],如果最短距离是10 ,那就是 grid[1][9] = 10。
那 节点1 到 节点9 的最短距离 是不是可以由 节点1 到节点5的最短距离 + 节点5到节点9的最短距离组成呢?
即 grid[1][9] = grid[1][5] + grid[5][9]
节点1 到节点5的最短距离 是不是可以有 节点1 到 节点3的最短距离 + 节点3 到 节点5 的最短距离组成呢?
即 grid[1][5] = grid[1][3] + grid[3][5]
以此类推,节点1 到 节点3的最短距离 可以由更小的区间组成。
那么这样我们是不是就找到了,子问题推导求出整体最优方案的递归关系呢。
节点1 到 节点9 的最短距离 可以由 节点1 到节点5的最短距离 + 节点5到节点9的最短距离组成, 也可以有 节点1 到节点7的最短距离 + 节点7 到节点9的最短距离的距离组成。
那么选哪个呢?
是不是 要选一个最小的,毕竟是求最短路。
此时我们已经接近明确递归公式了。
之前在讲解动态规划的时候,给出过动规五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
那么接下来我们还是用这五部来给大家讲解 Floyd。
1、确定dp数组(dp table)以及下标的含义
这里我们用 grid数组来存图,那就把dp数组命名为 grid。
grid[i][j][k] = m,表示 节点i 到 节点j 以[1...k] 集合中的一个节点为中间节点的最短距离为m。
可能有录友会想,凭什么就这么定义呢?
节点i 到 节点j 的最短距离为m,这句话可以理解,但 以[1...k]集合为中间节点就理解不辽了。
节点i 到 节点j 的最短路径中 一定是经过很多节点,那么这个集合用[1...k] 来表示。
你可以反过来想,节点i 到 节点j 中间一定经过很多节点,那么你能用什么方式来表述中间这么多节点呢?
所以 这里的k不能单独指某个节点,k 一定要表示一个集合,即[1...k] ,表示节点1 到 节点k 一共k个节点的集合。
2、确定递推公式
在上面的分析中我们已经初步感受到了递推的关系。
我们分两种情况:
- 节点i 到 节点j 的最短路径经过节点k
- 节点i 到 节点j 的最短路径不经过节点k
对于第一种情况,grid[i][j][k] = grid[i][k][k - 1] + grid[k][j][k - 1]
节点i 到 节点k 的最短距离 是不经过节点k,中间节点集合为[1...k-1],所以 表示为grid[i][k][k - 1]
节点k 到 节点j 的最短距离 也是不经过节点k,中间节点集合为[1...k-1],所以表示为 grid[k][j][k - 1]
第二种情况,grid[i][j][k] = grid[i][j][k - 1]
如果节点i 到 节点j的最短距离 不经过节点k,那么 中间节点集合[1...k-1],表示为 grid[i][j][k - 1]
因为我们是求最短路,对于这两种情况自然是取最小值。
即: grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1])
3、dp数组如何初始化
grid[i][j][k] = m,表示 节点i 到 节点j 以[1...k] 集合为中间节点的最短距离为m。
刚开始初始化k 是不确定的。
例如题目中只是输入边(节点2 -> 节点6,权值为3),那么grid[2][6][k] = 3,k需要填什么呢?
把k 填成1,那如何上来就知道 节点2 经过节点1 到达节点6的最短距离是多少 呢。
所以 只能 把k 赋值为 0,本题 节点0 是无意义的,节点是从1 到 n。
这样我们在下一轮计算的时候,就可以根据 grid[i][j][0] 来计算 grid[i][j][1],此时的 grid[i][j][1] 就是 节点i 经过节点1 到达 节点j 的最小距离了。
grid数组是一个三维数组,那么我们初始化的数据在 i 与 j 构成的平层,如图:
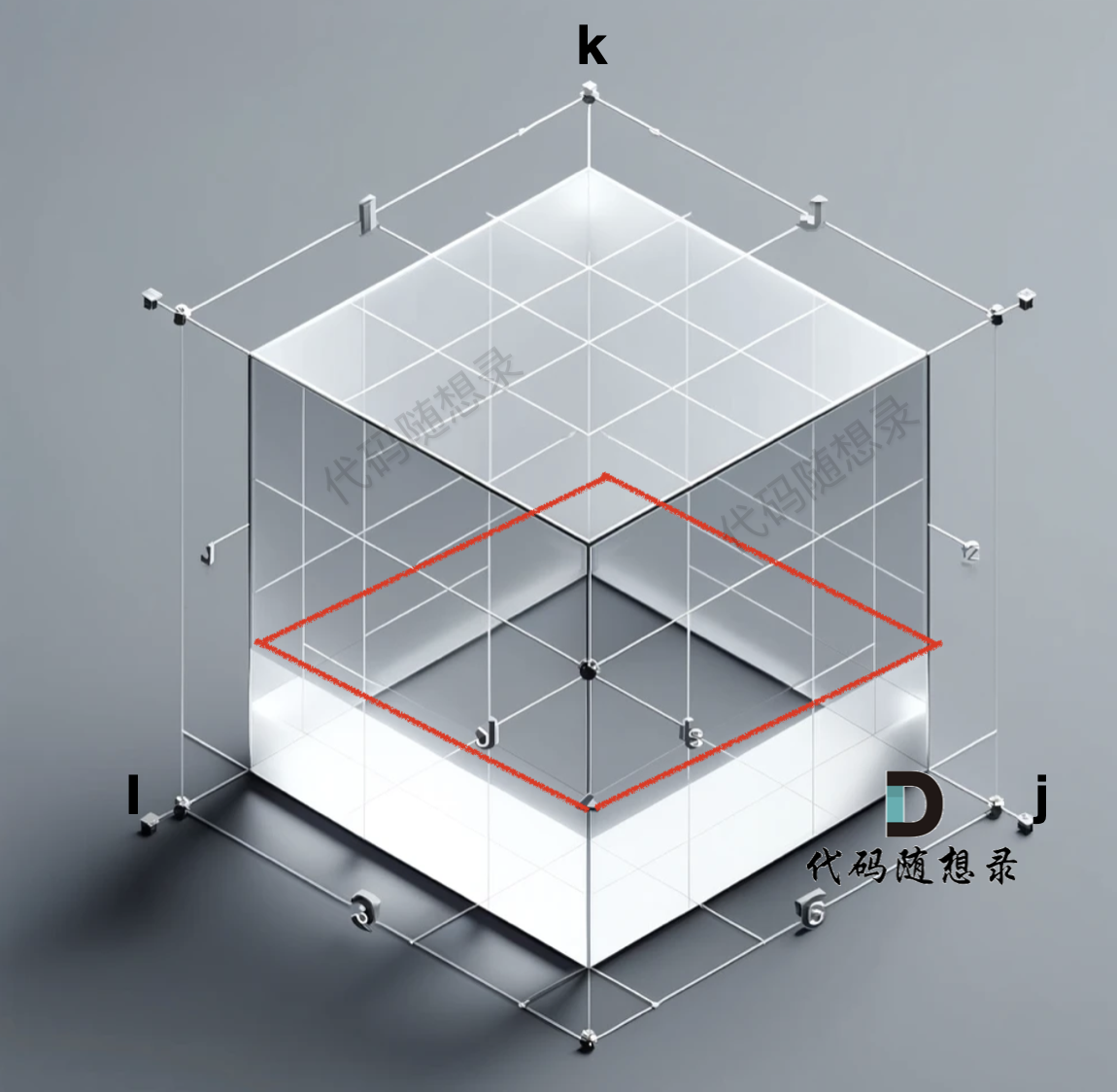
红色的 底部一层是我们初始化好的数据,注意:从三维角度去看初始化的数据很重要,下面我们在聊遍历顺序的时候还会再讲。
所以初始化代码:
vector<vector<vector<int>>> grid(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10005))); // C++定义了一个三位数组,10005是因为边的最大距离是10^4
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2][0] = val;
grid[p2][p1][0] = val; // 注意这里是双向图
}
2
3
4
5
6
7
8
grid数组中其他元素数值应该初始化多少呢?
本题求的是最小值,所以输入数据没有涉及到的节点的情况都应该初始为一个最大数。
这样才不会影响,每次计算去最小值的时候 初始值对计算结果的影响。
所以grid数组的定义可以是:
// C++写法,定义了一个三位数组,10005是因为边的最大距离是10^4
vector<vector<vector<int>>> grid(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10005)));
2
3
4、确定遍历顺序
从递推公式:grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1]) 可以看出,我们需要三个for循环,分别遍历i,j 和k
而 k 依赖于 k - 1, i 和j 的到 并不依赖与 i - 1 或者 j - 1 等等。
那么这三个for的嵌套顺序应该是什么样的呢?
我们来看初始化,我们是把 k =0 的 i 和j 对应的数值都初始化了,这样才能去计算 k = 1 的时候 i 和 j 对应的数值。
这就好比是一个三维坐标,i 和j 是平层,而k 是 垂直向上 的。
遍历的顺序是从底向上 一层一层去遍历。
所以遍历k 的for循环一定是在最外面,这样才能一层一层去遍历。如图:
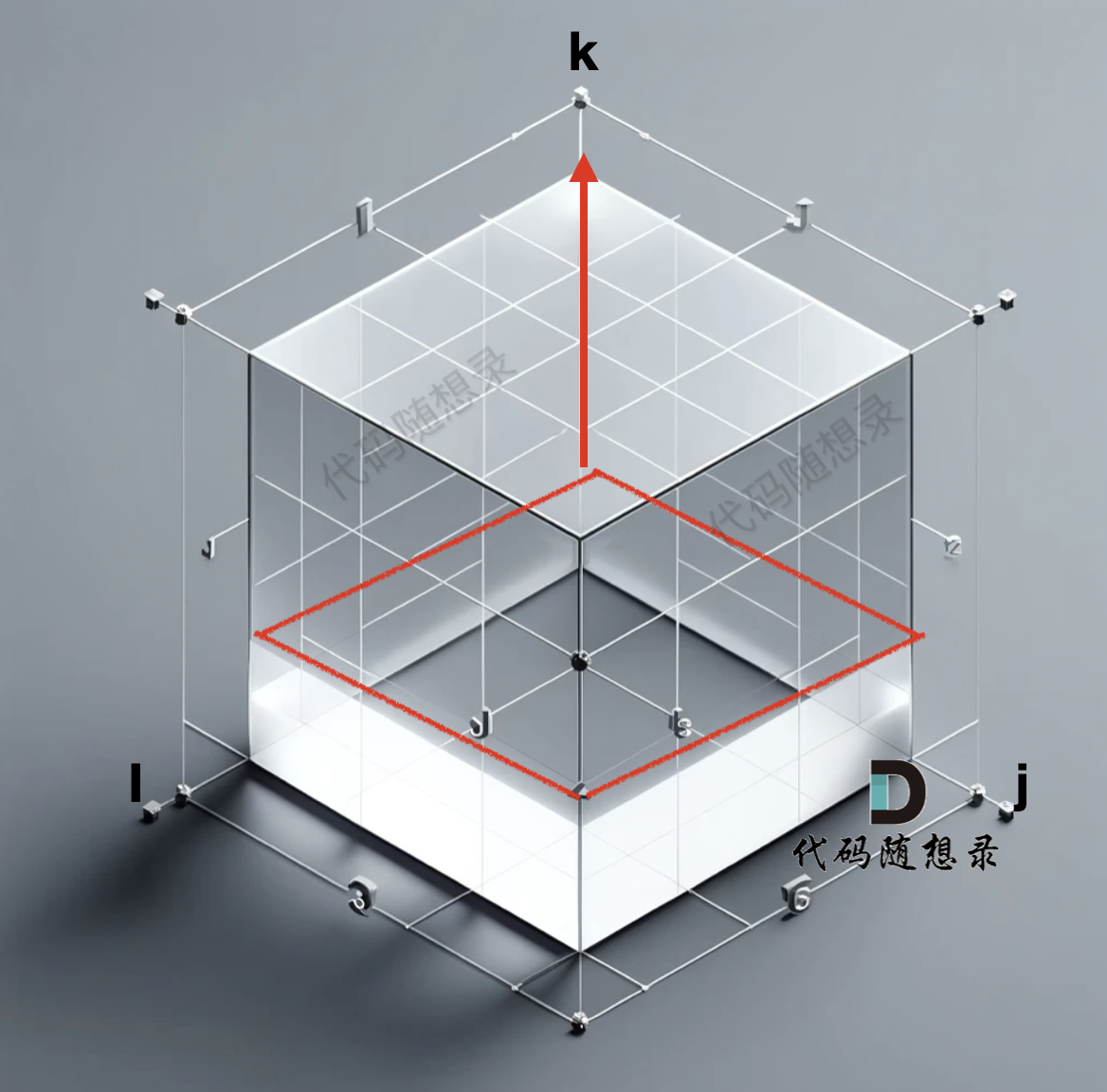
至于遍历 i 和 j 的话,for 循环的先后顺序无所谓。
代码如下:
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1]);
}
}
}
2
3
4
5
6
7
有录友可能想,难道 遍历k 放在最里层就不行吗?
k 放在最里层,代码是这样:
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1]);
}
}
}
2
3
4
5
6
7
此时就遍历了 j 与 k 形成一个平面,i 则是纵面,那遍历 就是这样的:
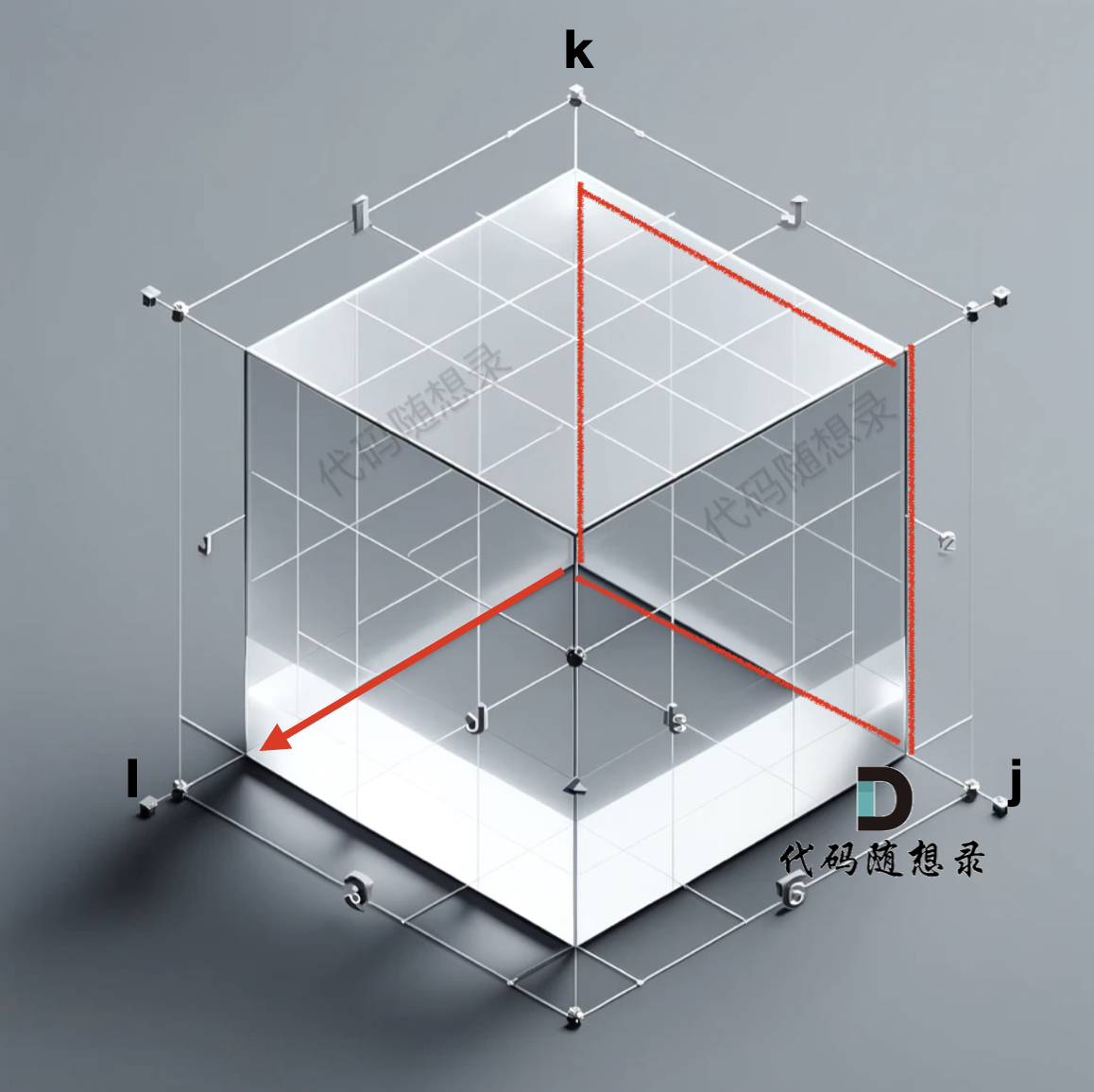
而我们初始化的数据 是 k 为0, i 和 j 形成的平面做初始化,如果以 k 和 j 形成的平面去一层一层遍历,就造成了 递推公式 用不上上一轮计算的结果,从而导致结果不对(初始化的部分是 i 与j 形成的平面,在初始部分有讲过)。
我再给大家举一个测试用例
5 4
1 2 10
1 3 1
3 4 1
4 2 1
1
1 2
2
3
4
5
6
7
就是图:
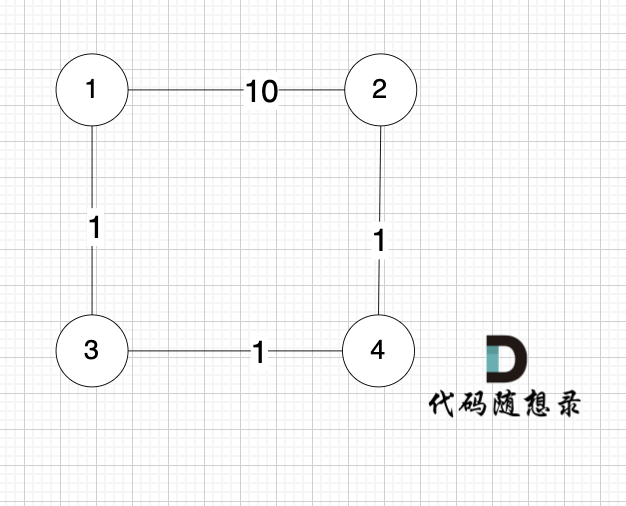
求节点1 到 节点 2 的最短距离,运行结果是 10 ,但正确的结果很明显是3。
为什么呢?
因为 k 放在最里面,先就把 节点1 和 节点 2 的最短距离就确定了,后面再也不会计算节点 1 和 节点 2的距离,同时也不会基于 初始化或者之前计算过的结果来计算,即:不会考虑 节点1 到 节点3, 节点3 到节点 4,节点4到节点2 的距离。
造成这一原因,是 在三维立体坐标中, 我们初始化的是 i 和 i 在k 为0 所构成的平面,但遍历的时候 是以 j 和 k构成的平面以 i 为垂直方向去层次遍历。
而遍历k 的for循环如果放在中间呢,同样是 j 与k 行程一个平面,i 是纵面,遍历的也是这样:

同样不能完全用上初始化 和 上一层计算的结果。
根据这个情况再举一个例子:
5 2
1 2 1
2 3 10
1
1 3
2
3
4
5
图:
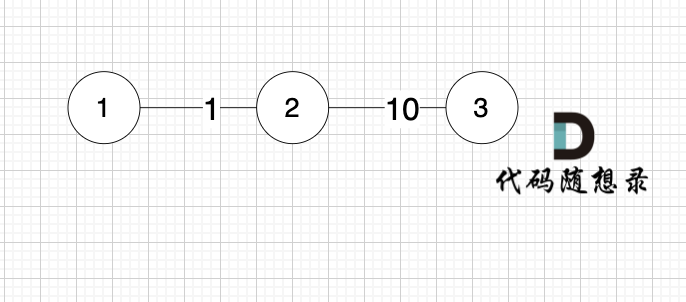
求 节点1 到节点3 的最短距离,如果k循环放中间,程序的运行结果是 -1,也就是不能到达节点3。
在计算 grid[i][j][k] 的时候,需要基于 grid[i][k][k-1] 和 grid[k][j][k-1]的数值。
也就是 计算 grid[1][3][2] (表示节点1 到 节点3,经过节点2) 的时候,需要基于 grid[1][2][1] 和 grid[2][3][1]的数值,而 我们初始化,只初始化了 k为0 的那一层。
造成这一原因 依然是 在三维立体坐标中, 我们初始化的是 i 和 j 在k 为0 所构成的平面,但遍历的时候 是以 j 和 k构成的平面以 i 为垂直方向去层次遍历。
很多录友对于 floyd算法的遍历顺序搞不懂,其实 是没有从三维的角度去思考,同时我把三维立体图给大家画出来,遍历顺序标出来,大家就很容易想明白,为什么 k 放在最外层 才能用上 初始化和上一轮计算的结果了。
5、举例推导dp数组
这里涉及到 三维矩阵,可以一层一层打印出来去分析,例如k=0 的这一层,k = 1的这一层,但一起把三维带数据的图画出来其实不太好画。
# 代码如下
以上分析完毕,最后代码如下:
#include <iostream>
#include <vector>
#include <list>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<vector<int>>> grid(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10005))); // 因为边的最大距离是10^4
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2][0] = val;
grid[p2][p1][0] = val; // 注意这里是双向图
}
// 开始 floyd
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1]);
}
}
}
// 输出结果
int z, start, end;
cin >> z;
while (z--) {
cin >> start >> end;
if (grid[start][end][n] == 10005) cout << -1 << endl;
else cout << grid[start][end][n] << endl;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 空间优化
这里 我们可以做一下 空间上的优化,从滚动数组的角度来看,我们定义一个 grid[n + 1][ n + 1][2] 这么大的数组就可以,因为k 只是依赖于 k-1的状态,并不需要记录k-2,k-3,k-4 等等这些状态。
那么我们只需要记录 grid[i][j][1] 和 grid[i][j][0] 就好,之后就是 grid[i][j][1] 和 grid[i][j][0] 交替滚动。
在进一步想,如果本层计算(本层计算即k相同,从三维角度来讲) gird[i][j] 用到了 本层中刚计算好的 grid[i][k] 会有什么问题吗?
如果 本层刚计算好的 grid[i][k] 比上一层 (即k-1层)计算的 grid[i][k] 小,说明确实有 i 到 k 的更短路径,那么基于 更小的 grid[i][k] 去计算 gird[i][j] 没有问题。
如果 本层刚计算好的 grid[i][k] 比上一层 (即k-1层)计算的 grid[i][k] 大, 这不可能,因为这样也不会做更新 grid[i][k]的操作。
所以本层计算中,使用了本层计算过的 grid[i][k] 和 grid[k][j] 是没问题的。
那么就没必要区分,grid[i][k] 和 grid[k][j] 是 属于 k - 1 层的呢,还是 k 层的。
所以递归公式可以为:
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
基于二维数组的本题代码为:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid(n + 1, vector<int>(n + 1, 10005)); // 因为边的最大距离是10^4
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
grid[p2][p1] = val; // 注意这里是双向图
}
// 开始 floyd
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
}
}
}
// 输出结果
int z, start, end;
cin >> z;
while (z--) {
cin >> start >> end;
if (grid[start][end] == 10005) cout << -1 << endl;
else cout << grid[start][end] << endl;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
- 时间复杂度: O(n^3)
- 空间复杂度:O(n^2)
# 总结
本期如果上来只用二维数组来讲的话,其实更容易,但遍历顺序那里用二维数组其实是讲不清楚的,所以我直接用三维数组来讲,目的是将遍历顺序这里讲清楚。
理解了遍历顺序才是floyd算法最精髓的地方。
floyd算法的时间复杂度相对较高,适合 稠密图且源点较多的情况。
如果是稀疏图,floyd是从节点的角度去计算了,例如 图中节点数量是 1000,就一条边,那 floyd的时间复杂度依然是 O(n^3) 。
如果 源点少,其实可以 多次dijsktra 求源点到终点。
# 其他语言版本
# Java
- 基于三维数组的Floyd算法
public class FloydBase {
// public static int MAX_VAL = Integer.MAX_VALUE;
public static int MAX_VAL = 10005; // 边的最大距离是10^4(不选用Integer.MAX_VALUE是为了避免相加导致数值溢出)
public static void main(String[] args) {
// 输入控制
Scanner sc = new Scanner(System.in);
System.out.println("1.输入N M");
int n = sc.nextInt();
int m = sc.nextInt();
System.out.println("2.输入M条边");
// ① dp定义(grid[i][j][k] 节点i到节点j 可能经过节点K(k∈[1,n]))的最短路径
int[][][] grid = new int[n + 1][n + 1][n + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 0; k <= n; k++) {
grid[i][j][k] = grid[j][i][k] = MAX_VAL; // 其余设置为最大值
}
}
}
// ② dp 推导:grid[i][j][k] = min{grid[i][k][k-1] + grid[k][j][k-1], grid[i][j][k-1]}
while (m-- > 0) {
int u = sc.nextInt();
int v = sc.nextInt();
int weight = sc.nextInt();
grid[u][v][0] = grid[v][u][0] = weight; // 初始化(处理k=0的情况) ③ dp初始化
}
// ④ dp推导:floyd 推导
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j][k] = Math.min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1]);
}
}
}
System.out.println("3.输入[起点-终点]计划个数");
int x = sc.nextInt();
System.out.println("4.输入每个起点src 终点dst");
while (x-- > 0) {
int src = sc.nextInt();
int dst = sc.nextInt();
// 根据floyd推导结果输出计划路径的最小距离
if (grid[src][dst][n] == MAX_VAL) {
System.out.println("-1");
} else {
System.out.println(grid[src][dst][n]);
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# Python
基于三维数组的Floyd
if __name__ == '__main__':
max_int = 10005 # 设置最大路径,因为边最大距离为10^4
n, m = map(int, input().split())
grid = [[[max_int] * (n+1) for _ in range(n+1)] for _ in range(n+1)] # 初始化三维dp数组
for _ in range(m):
p1, p2, w = map(int, input().split())
grid[p1][p2][0] = w
grid[p2][p1][0] = w
# 开始floyd
for k in range(1, n+1):
for i in range(1, n+1):
for j in range(1, n+1):
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1])
# 输出结果
z = int(input())
for _ in range(z):
start, end = map(int, input().split())
if grid[start][end][n] == max_int:
print(-1)
else:
print(grid[start][end][n])
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
基于二维数组的Floyd
if __name__ == '__main__':
max_int = 10005 # 设置最大路径,因为边最大距离为10^4
n, m = map(int, input().split())
grid = [[max_int]*(n+1) for _ in range(n+1)] # 初始化二维dp数组
for _ in range(m):
p1, p2, val = map(int, input().split())
grid[p1][p2] = val
grid[p2][p1] = val
# 开始floyd
for k in range(1, n+1):
for i in range(1, n+1):
for j in range(1, n+1):
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j])
# 输出结果
z = int(input())
for _ in range(z):
start, end = map(int, input().split())
if grid[start][end] == max_int:
print(-1)
else:
print(grid[start][end])
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

评论
验证登录状态...