- 做项目(多个C++、Java、Go、测开、前端项目) (opens new window)
- 刷算法(两个月高强度学算法) (opens new window)
- 背八股(40天挑战高频面试题) (opens new window)
和子集问题有点像,但又处处是陷阱
# 491.递增子序列
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
- 输入: [4, 6, 7, 7]
- 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
# 算法公开课
《代码随想录》算法视频公开课 (opens new window):回溯算法精讲,树层去重与树枝去重 | LeetCode:491.递增子序列 (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
# 思路
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
这又是子集,又是去重,是不是不由自主的想起了刚刚讲过的90.子集II (opens new window)。
就是因为太像了,更要注意差别所在,要不就掉坑里了!
在90.子集II (opens new window)中我们是通过排序,再加一个标记数组来达到去重的目的。
而本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑!
本题给出的示例,还是一个有序数组 [4, 6, 7, 7],这更容易误导大家按照排序的思路去做了。
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
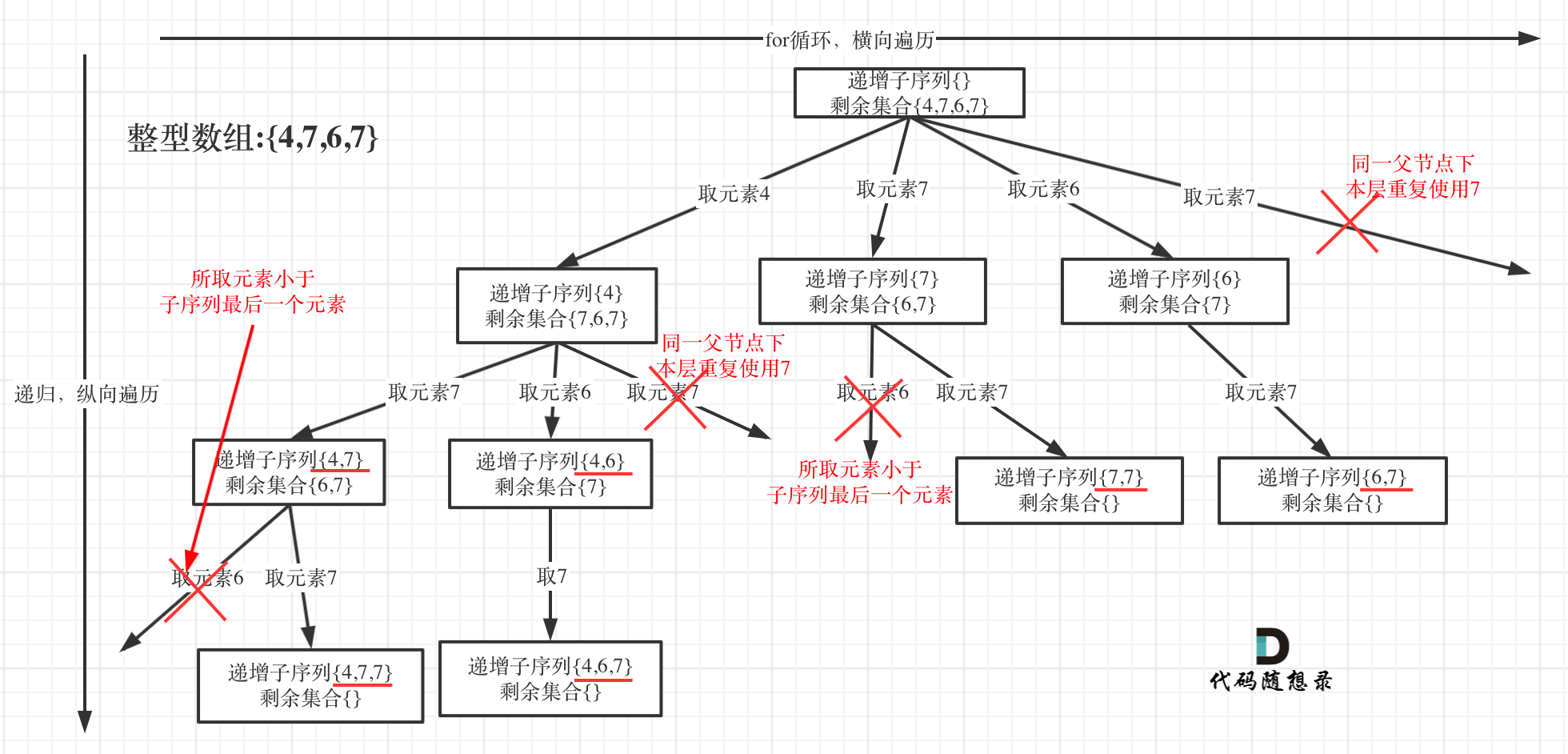
# 回溯三部曲
- 递归函数参数
本题求子序列,很明显一个元素不能重复使用,所以需要startIndex,调整下一层递归的起始位置。
代码如下:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex)
2
3
- 终止条件
本题其实类似求子集问题,也是要遍历树形结构找每一个节点,所以和回溯算法:求子集问题! (opens new window)一样,可以不加终止条件,startIndex每次都会加1,并不会无限递归。
但本题收集结果有所不同,题目要求递增子序列大小至少为2,所以代码如下:
if (path.size() > 1) {
result.push_back(path);
// 注意这里不要加return,因为要取树上的所有节点
}
2
3
4
- 单层搜索逻辑
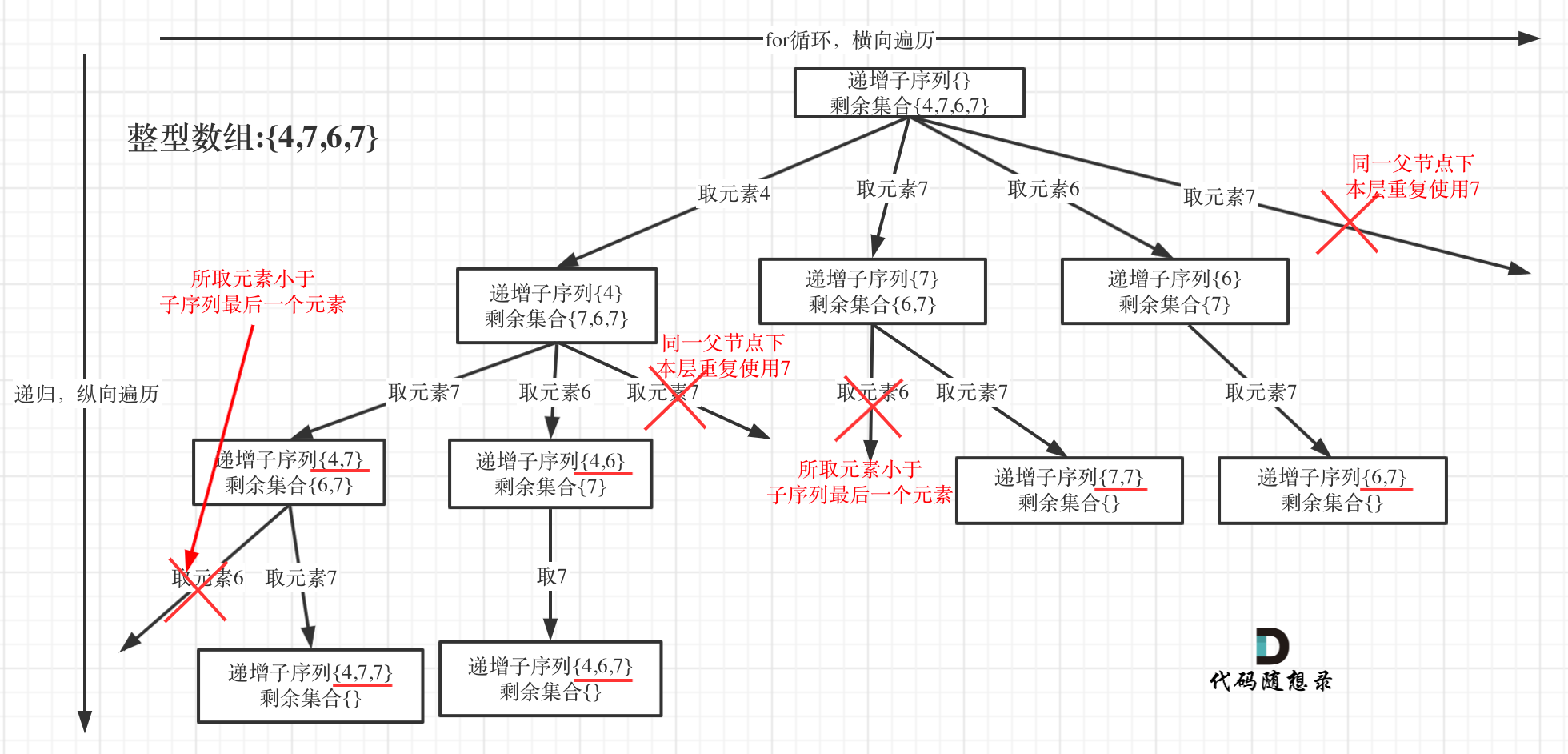 在图中可以看出,同一父节点下的同层上使用过的元素就不能再使用了
在图中可以看出,同一父节点下的同层上使用过的元素就不能再使用了
那么单层搜索代码如下:
unordered_set<int> uset; // 使用set来对本层元素进行去重
for (int i = startIndex; i < nums.size(); i++) {
if ((!path.empty() && nums[i] < path.back())
|| uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
2
3
4
5
6
7
8
9
10
11
对于已经习惯写回溯的同学,看到递归函数上面的uset.insert(nums[i]);,下面却没有对应的pop之类的操作,应该很不习惯吧
这也是需要注意的点,unordered_set<int> uset; 是记录本层元素是否重复使用,新的一层uset都会重新定义(清空),所以要知道uset只负责本层!
最后整体C++代码如下:
// 版本一
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
if (path.size() > 1) {
result.push_back(path);
// 注意这里不要加return,要取树上的节点
}
unordered_set<int> uset; // 使用set对本层元素进行去重
for (int i = startIndex; i < nums.size(); i++) {
if ((!path.empty() && nums[i] < path.back())
|| uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> findSubsequences(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n)
# 优化
以上代码用我用了unordered_set<int>来记录本层元素是否重复使用。
其实用数组来做哈希,效率就高了很多。
注意题目中说了,数值范围[-100,100],所以完全可以用数组来做哈希。
程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且每次重新定义set,insert的时候其底层的符号表也要做相应的扩充,也是费事的。
那么优化后的代码如下:
// 版本二
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
if (path.size() > 1) {
result.push_back(path);
}
int used[201] = {0}; // 这里使用数组来进行去重操作,题目说数值范围[-100, 100]
for (int i = startIndex; i < nums.size(); i++) {
if ((!path.empty() && nums[i] < path.back())
|| used[nums[i] + 100] == 1) {
continue;
}
used[nums[i] + 100] = 1; // 记录这个元素在本层用过了,本层后面不能再用了
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> findSubsequences(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
这份代码在leetcode上提交,要比版本一耗时要好的多。
所以正如在哈希表:总结篇!(每逢总结必经典) (opens new window)中说的那样,数组,set,map都可以做哈希表,而且数组干的活,map和set都能干,但如果数值范围小的话能用数组尽量用数组。
# 总结
本题题解清一色都说是深度优先搜索,但我更倾向于说它用回溯法,而且本题我也是完全使用回溯法的逻辑来分析的。
相信大家在本题中处处都能看到是回溯算法:求子集问题(二) (opens new window)的身影,但处处又都是陷阱。
对于养成思维定式或者套模板套嗨了的同学,这道题起到了很好的警醒作用。更重要的是拓展了大家的思路!
# 其他语言版本
# Java
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backTracking(nums, 0);
return result;
}
private void backTracking(int[] nums, int startIndex){
if(path.size() >= 2)
result.add(new ArrayList<>(path));
HashSet<Integer> hs = new HashSet<>();
for(int i = startIndex; i < nums.length; i++){
if(!path.isEmpty() && path.get(path.size() -1 ) > nums[i] || hs.contains(nums[i]))
continue;
hs.add(nums[i]);
path.add(nums[i]);
backTracking(nums, i + 1);
path.remove(path.size() - 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
private List<Integer> path = new ArrayList<>();
private List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backtracking(nums,0);
return res;
}
private void backtracking (int[] nums, int start) {
if (path.size() > 1) {
res.add(new ArrayList<>(path));
}
int[] used = new int[201];
for (int i = start; i < nums.length; i++) {
if (!path.isEmpty() && nums[i] < path.get(path.size() - 1) ||
(used[nums[i] + 100] == 1)) continue;
used[nums[i] + 100] = 1;
path.add(nums[i]);
backtracking(nums, i + 1);
path.remove(path.size() - 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//法二:使用map
class Solution {
//结果集合
List<List<Integer>> res = new ArrayList<>();
//路径集合
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
getSubsequences(nums,0);
return res;
}
private void getSubsequences( int[] nums, int start ) {
if(path.size()>1 ){
res.add( new ArrayList<>(path) );
// 注意这里不要加return,要取树上的节点
}
HashMap<Integer,Integer> map = new HashMap<>();
for(int i=start ;i < nums.length ;i++){
if(!path.isEmpty() && nums[i]< path.getLast()){
continue;
}
// 使用过了当前数字
if ( map.getOrDefault( nums[i],0 ) >=1 ){
continue;
}
map.put(nums[i],map.getOrDefault( nums[i],0 )+1);
path.add( nums[i] );
getSubsequences( nums,i+1 );
path.removeLast();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Python
回溯 利用set去重
class Solution:
def findSubsequences(self, nums):
result = []
path = []
self.backtracking(nums, 0, path, result)
return result
def backtracking(self, nums, startIndex, path, result):
if len(path) > 1:
result.append(path[:]) # 注意要使用切片将当前路径的副本加入结果集
# 注意这里不要加return,要取树上的节点
uset = set() # 使用集合对本层元素进行去重
for i in range(startIndex, len(nums)):
if (path and nums[i] < path[-1]) or nums[i] in uset:
continue
uset.add(nums[i]) # 记录这个元素在本层用过了,本层后面不能再用了
path.append(nums[i])
self.backtracking(nums, i + 1, path, result)
path.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
回溯 利用哈希表去重
class Solution:
def findSubsequences(self, nums):
result = []
path = []
self.backtracking(nums, 0, path, result)
return result
def backtracking(self, nums, startIndex, path, result):
if len(path) > 1:
result.append(path[:]) # 注意要使用切片将当前路径的副本加入结果集
used = [0] * 201 # 使用数组来进行去重操作,题目说数值范围[-100, 100]
for i in range(startIndex, len(nums)):
if (path and nums[i] < path[-1]) or used[nums[i] + 100] == 1:
continue # 如果当前元素小于上一个元素,或者已经使用过当前元素,则跳过当前元素
used[nums[i] + 100] = 1 # 标记当前元素已经使用过
path.append(nums[i]) # 将当前元素加入当前递增子序列
self.backtracking(nums, i + 1, path, result)
path.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Go
var (
res [][]int
path []int
)
func findSubsequences(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
dfs(nums, 0)
return res
}
func dfs(nums []int, start int) {
if len(path) >= 2 {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
used := make(map[int]bool, len(nums)) // 初始化used字典,用以对同层元素去重
for i := start; i < len(nums); i++ {
if used[nums[i]] { // 去重
continue
}
if len(path) == 0 || nums[i] >= path[len(path)-1] {
path = append(path, nums[i])
used[nums[i]] = true
dfs(nums, i+1)
path = path[:len(path)-1]
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# JavaScript
var findSubsequences = function(nums) {
let result = []
let path = []
function backtracing(startIndex) {
if(path.length > 1) {
result.push(path.slice())
}
let uset = []
for(let i = startIndex; i < nums.length; i++) {
if((path.length > 0 && nums[i] < path[path.length - 1]) || uset[nums[i] + 100]) {
continue
}
uset[nums[i] + 100] = true
path.push(nums[i])
backtracing(i + 1)
path.pop()
}
}
backtracing(0)
return result
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# TypeScript
function findSubsequences(nums: number[]): number[][] {
const resArr: number[][] = [];
backTracking(nums, 0, []);
return resArr;
function backTracking(nums: number[], startIndex: number, route: number[]): void {
let length: number = nums.length;
if (route.length >= 2) {
resArr.push(route.slice());
}
const usedSet: Set<number> = new Set();
for (let i = startIndex; i < length; i++) {
if (
nums[i] < route[route.length - 1] ||
usedSet.has(nums[i])
) continue;
usedSet.add(nums[i]);
route.push(nums[i]);
backTracking(nums, i + 1, route);
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Rust
回溯+哈希
use std::collections::HashSet;
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, start_index: usize) {
if path.len() > 1 { result.push(path.clone()); }
let len = nums.len();
let mut uset: HashSet<i32> = HashSet::new();
for i in start_index..len {
if (!path.is_empty() && nums[i] < *path.last().unwrap()) || uset.contains(&nums[i]) { continue; }
uset.insert(nums[i]);
path.push(nums[i]);
Self::backtracking(result, path, nums, i + 1);
path.pop();
}
}
pub fn find_subsequences(nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut path: Vec<i32> = Vec::new();
Self::backtracking(&mut result, &mut path, &nums, 0);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
回溯+数组
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, start_index: usize) {
if path.len() > 1 { result.push(path.clone()); }
let len = nums.len();
let mut used = [0; 201];
for i in start_index..len {
if (!path.is_empty() && nums[i] < *path.last().unwrap()) || used[(nums[i] + 100) as usize] == 1 { continue; }
used[(nums[i] + 100) as usize] = 1;
path.push(nums[i]);
Self::backtracking(result, path, nums, i + 1);
path.pop();
}
}
pub fn find_subsequences(nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut path: Vec<i32> = Vec::new();
Self::backtracking(&mut result, &mut path, &nums, 0);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C
int* path;
int pathTop;
int** ans;
int ansTop;
int* length;
//将当前path中的内容复制到ans中
void copy() {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
memcpy(tempPath, path, pathTop * sizeof(int));
length[ansTop] = pathTop;
ans[ansTop++] = tempPath;
}
//查找uset中是否存在值为key的元素
int find(int* uset, int usetSize, int key) {
int i;
for(i = 0; i < usetSize; i++) {
if(uset[i] == key)
return 1;
}
return 0;
}
void backTracking(int* nums, int numsSize, int startIndex) {
//当path中元素大于1个时,将path拷贝到ans中
if(pathTop > 1) {
copy();
}
int* uset = (int*)malloc(sizeof(int) * numsSize);
int usetTop = 0;
int i;
for(i = startIndex; i < numsSize; i++) {
//若当前元素小于path中最后一位元素 || 在树的同一层找到了相同的元素,则continue
if((pathTop > 0 && nums[i] < path[pathTop - 1]) || find(uset, usetTop, nums[i]))
continue;
//将当前元素放入uset
uset[usetTop++] = nums[i];
//将当前元素放入path
path[pathTop++] = nums[i];
backTracking(nums, numsSize, i + 1);
//回溯
pathTop--;
}
}
int** findSubsequences(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
//辅助数组初始化
path = (int*)malloc(sizeof(int) * numsSize);
ans = (int**)malloc(sizeof(int*) * 33000);
length = (int*)malloc(sizeof(int*) * 33000);
pathTop = ansTop = 0;
backTracking(nums, numsSize, 0);
//设置数组中返回元素个数,以及每个一维数组的长度
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = length[i];
}
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# Swift
func findSubsequences(_ nums: [Int]) -> [[Int]] {
var result = [[Int]]()
var path = [Int]()
func backtracking(startIndex: Int) {
// 收集结果,但不返回,因为后续还要以此基础拼接
if path.count > 1 {
result.append(path)
}
var uset = Set<Int>()
let end = nums.count
guard startIndex < end else { return } // 终止条件
for i in startIndex ..< end {
let num = nums[i]
if uset.contains(num) { continue } // 跳过重复元素
if !path.isEmpty, num < path.last! { continue } // 确保递增
uset.insert(num) // 通过set记录
path.append(num) // 处理:收集元素
backtracking(startIndex: i + 1) // 元素不重复访问
path.removeLast() // 回溯
}
}
backtracking(startIndex: 0)
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Scala
object Solution {
import scala.collection.mutable
def findSubsequences(nums: Array[Int]): List[List[Int]] = {
var result = mutable.ListBuffer[List[Int]]()
var path = mutable.ListBuffer[Int]()
def backtracking(startIndex: Int): Unit = {
// 集合元素大于1,添加到结果集
if (path.size > 1) {
result.append(path.toList)
}
var used = new Array[Boolean](201)
// 使用循环守卫,当前层没有用过的元素才有资格进入回溯
for (i <- startIndex until nums.size if !used(nums(i) + 100)) {
// 如果path没元素或 当前循环的元素比path的最后一个元素大,则可以进入回溯
if (path.size == 0 || (!path.isEmpty && nums(i) >= path(path.size - 1))) {
used(nums(i) + 100) = true
path.append(nums(i))
backtracking(i + 1)
path.remove(path.size - 1)
}
}
}
backtracking(0)
result.toList
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# C#
public class Solution {
public IList<IList<int>> res = new List<IList<int>>();
public IList<int> path = new List<int>();
public IList<IList<int>> FindSubsequences(int[] nums) {
BackTracking(nums, 0);
return res;
}
public void BackTracking(int[] nums, int start){
if(path.Count >= 2){
res.Add(new List<int>(path));
}
HashSet<int> hs = new HashSet<int>();
for(int i = start; i < nums.Length; i++){
if(path.Count > 0 && path[path.Count - 1] > nums[i] || hs.Contains(nums[i])){
continue;
}
hs.Add(nums[i]);
path.Add(nums[i]);
BackTracking(nums, i + 1);
path.RemoveAt(path.Count - 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
