# 本周小结!(贪心算法系列二)
# 周一
一说到股票问题,一般都会想到动态规划,其实有时候贪心更有效!
在贪心算法:买卖股票的最佳时机II (opens new window)中,讲到只能多次买卖一支股票,如何获取最大利润。
这道题目理解利润拆分是关键点! 不要整块的去看,而是把整体利润拆为每天的利润,就很容易想到贪心了。
局部最优:只收集每天的正利润,全局最优:得到最大利润。
如果正利润连续上了,相当于连续持有股票,而本题并不需要计算具体的区间。
如图:
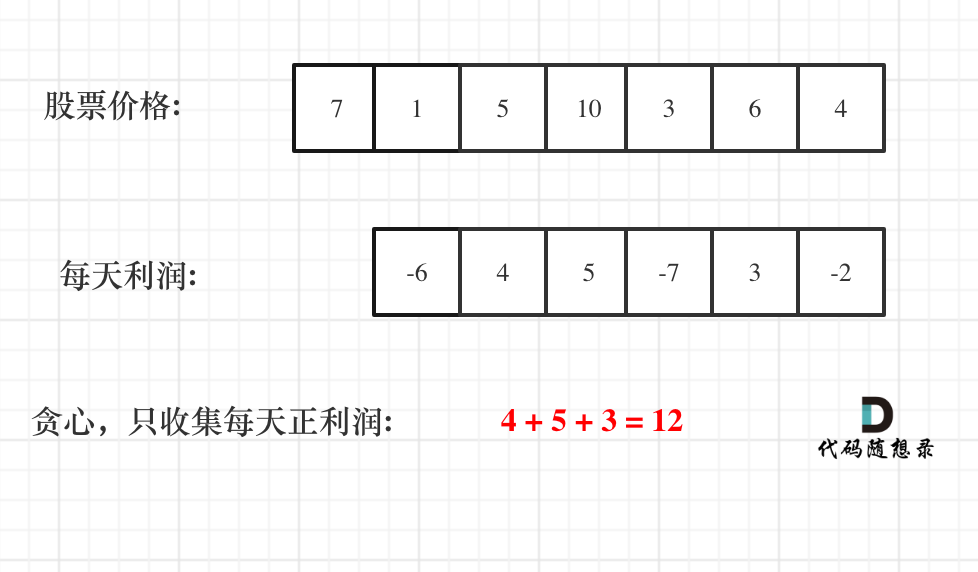
# 周二
在贪心算法:跳跃游戏 (opens new window)中是给你一个数组看能否跳到终点。
本题贪心的关键是:不用拘泥于每次究竟跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!
贪心算法局部最优解:移动下标每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点
如果覆盖范围覆盖到了终点,就表示一定可以跳过去。
如图:
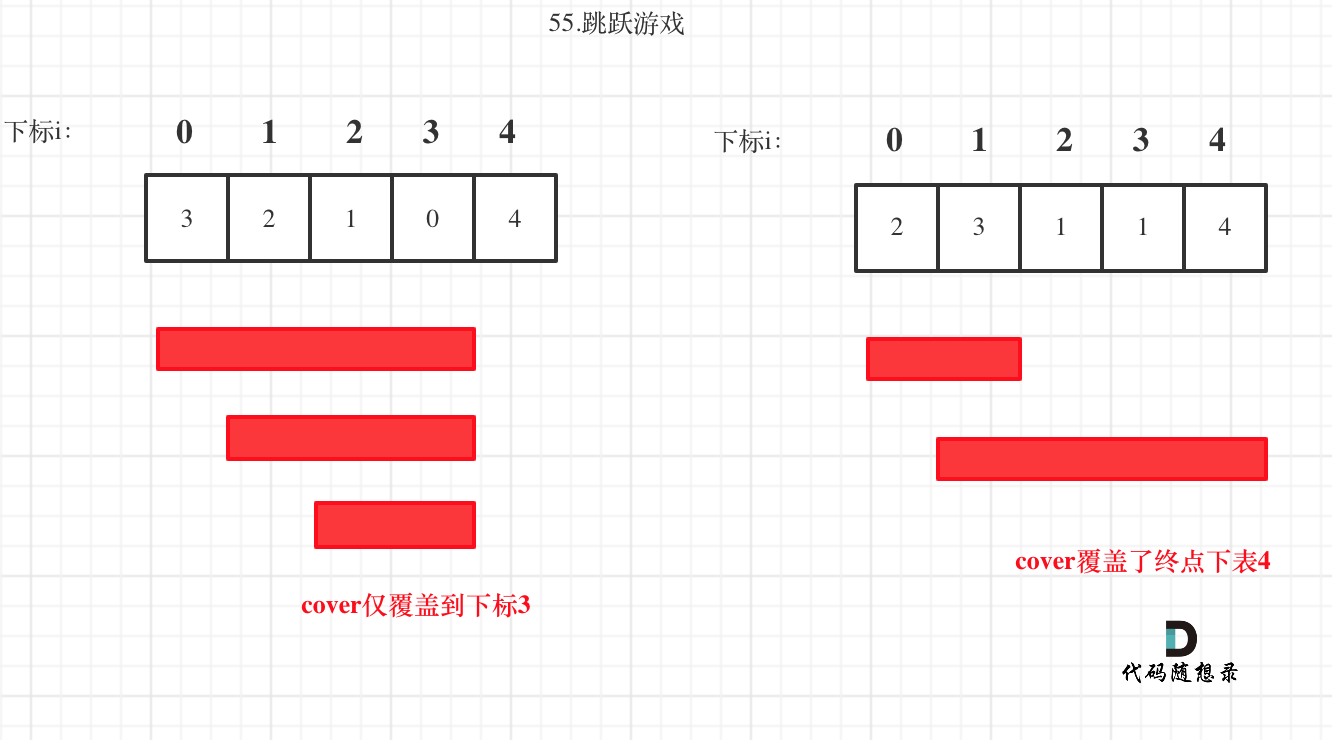
# 周三
这道题目:贪心算法:跳跃游戏II (opens new window)可就有点难了。
本题解题关键在于:以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点。
那么局部最优:求当前这步的最大覆盖,那么尽可能多走,到达覆盖范围的终点,只需要一步。整体最优:达到终点,步数最少。
如图:
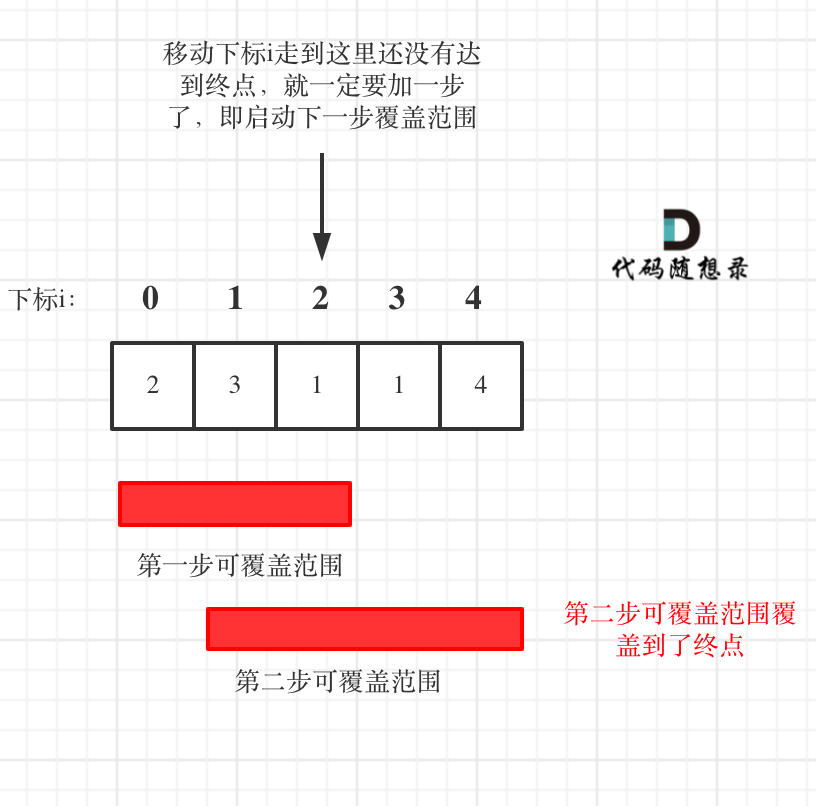
注意:图中的移动下标是到当前这步覆盖的最远距离(下标2的位置),此时没有到终点,只能增加第二步来扩大覆盖范围。
在贪心算法:跳跃游戏II (opens new window)中我给出了两个版本的代码。
其实本质都是超过当前覆盖范围,步数就加一,但版本一需要考虑当前覆盖最远距离下标是不是数组终点的情况。
而版本二就比较统一的,超过范围,步数就加一,但在移动下标的范围了做了文章。
即如果覆盖最远距离下标是倒数第二点:直接加一就行,默认一定可以到终点。如图:
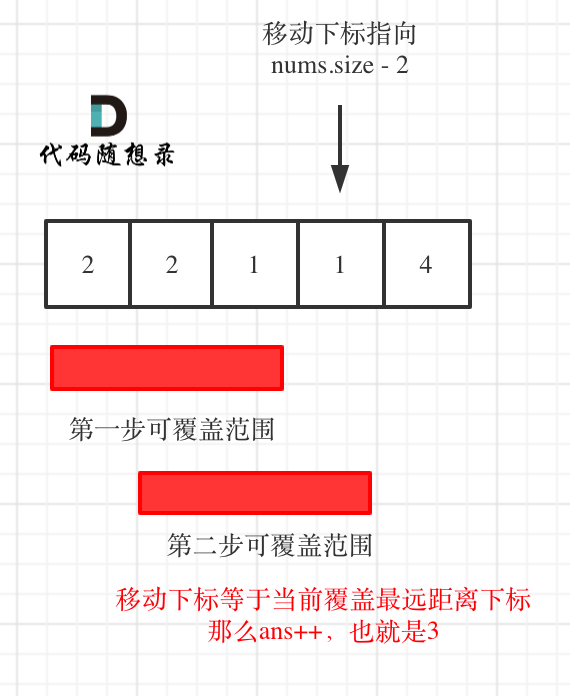
如果覆盖最远距离下标不是倒数第二点,说明本次覆盖已经到终点了。如图:
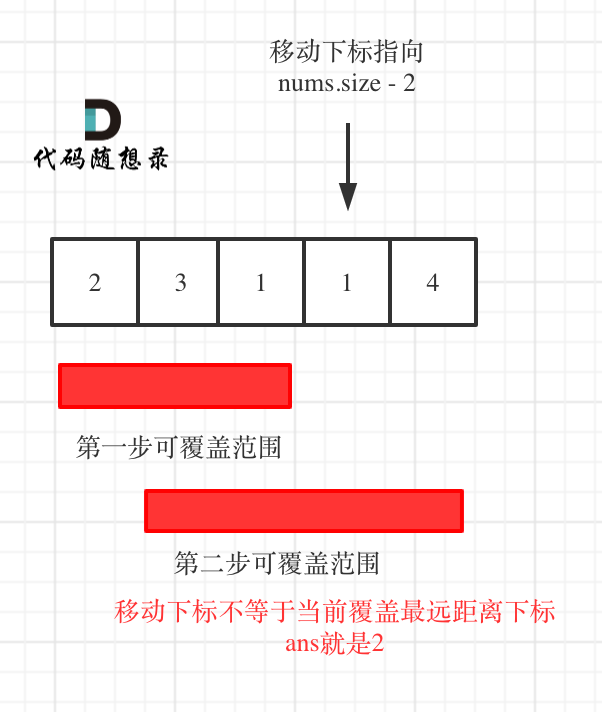
有的录友认为版本一好理解,有的录友认为版本二好理解,其实掌握一种就可以了,也不用非要比拼一下代码的简洁性,简洁程度都差不多了。
我个人倾向于版本一的写法,思路清晰一点,版本二会有点绕。
# 周四
这道题目:贪心算法:K次取反后最大化的数组和 (opens new window)就比较简单了,用简单题来讲一讲贪心的思想。
这里其实用了两次贪心!
第一次贪心:局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。
处理之后,如果K依然大于0,此时的问题是一个有序正整数序列,如何转变K次正负,让 数组和 达到最大。
第二次贪心:局部最优:只找数值最小的正整数进行反转,当前数值可以达到最大(例如正整数数组{5, 3, 1},反转1 得到-1 比 反转5得到的-5 大多了),全局最优:整个 数组和 达到最大。
例外一位录友留言给出一个很好的建议,因为文中是使用快排,仔细看题,题目中限定了数据范围是正负一百,所以可以使用桶排序,这样时间复杂度就可以优化为$O(n)$了。但可能代码要复杂一些了。
# 总结
大家会发现本周的代码其实都简单,但思路却很巧妙,并不容易写出来。
如果是第一次接触的话,其实很难想出来,就是接触过之后就会了,所以大家不用感觉自己想不出来而烦躁。
相信此时大家现在对贪心算法又有一个新的认识了,加油💪

