代码随想录

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

相对于贪心算法：跳跃游戏 (opens new window)难了不少，做好心理准备！

# 45.跳跃游戏 II

力扣题目链接 (opens new window)

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

  • 输入: [2,3,1,1,4]
  • 输出: 2
  • 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳  1  步，然后跳  3  步到达数组的最后一个位置。

说明: 假设你总是可以到达数组的最后一个位置。

# 算法公开课

《代码随想录》算法视频公开课 (opens new window)：贪心算法，最少跳几步还得看覆盖范围 | LeetCode： 45.跳跃游戏 II (opens new window)，相信结合视频在看本篇题解，更有助于大家对本题的理解。

# 思路

本题相对于55.跳跃游戏 (opens new window)还是难了不少。

但思路是相似的，还是要看最大覆盖范围。

本题要计算最少步数，那么就要想清楚什么时候步数才一定要加一呢？

贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最少步数。

思路虽然是这样，但在写代码的时候还不能真的能跳多远就跳多远，那样就不知道下一步最远能跳到哪里了。

所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最少步数！

这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

如图：

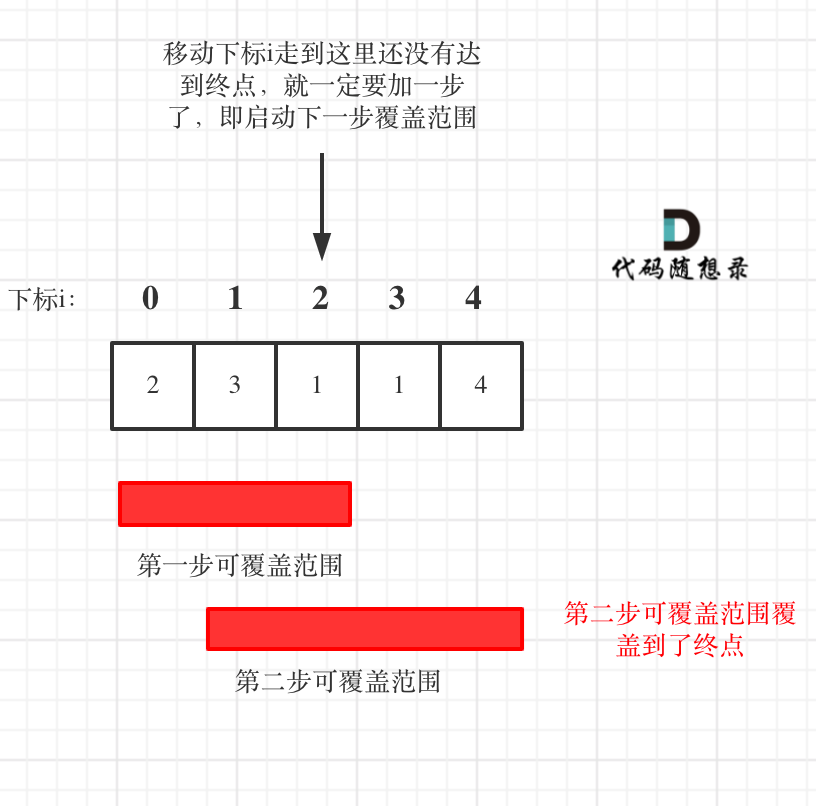
45.跳跃游戏II

图中覆盖范围的意义在于，只要红色的区域，最多两步一定可以到！（不用管具体怎么跳，反正一定可以跳到）

# 方法一

从图中可以看出来，就是移动下标达到了当前覆盖的最远距离下标时，步数就要加一，来增加覆盖距离。最后的步数就是最少步数。

这里还是有个特殊情况需要考虑，当移动下标达到了当前覆盖的最远距离下标时

  • 如果当前覆盖最远距离下标不是是集合终点，步数就加一，还需要继续走。
  • 如果当前覆盖最远距离下标就是是集合终点，步数不用加一，因为不能再往后走了。

C++代码如下：（详细注释）

// 版本一
class Solution {
public:
    int jump(vector<int>& nums) {
        if (nums.size() == 1) return 0;
        int curDistance = 0;    // 当前覆盖最远距离下标
        int ans = 0;            // 记录走的最大步数
        int nextDistance = 0;   // 下一步覆盖最远距离下标
        for (int i = 0; i < nums.size(); i++) {
            nextDistance = max(nums[i] + i, nextDistance);  // 更新下一步覆盖最远距离下标
            if (i == curDistance) {                         // 遇到当前覆盖最远距离下标
                ans++;                                  // 需要走下一步
                curDistance = nextDistance;             // 更新当前覆盖最远距离下标（相当于加油了）
                if (nextDistance >= nums.size() - 1) break;  // 当前覆盖最远距到达集合终点，不用做ans++操作了，直接结束
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  • 时间复杂度: O(n)
  • 空间复杂度: O(1)

# 方法二

依然是贪心，思路和方法一差不多，代码可以简洁一些。

针对于方法一的特殊情况，可以统一处理，即：移动下标只要遇到当前覆盖最远距离的下标，直接步数加一，不考虑是不是终点的情况。

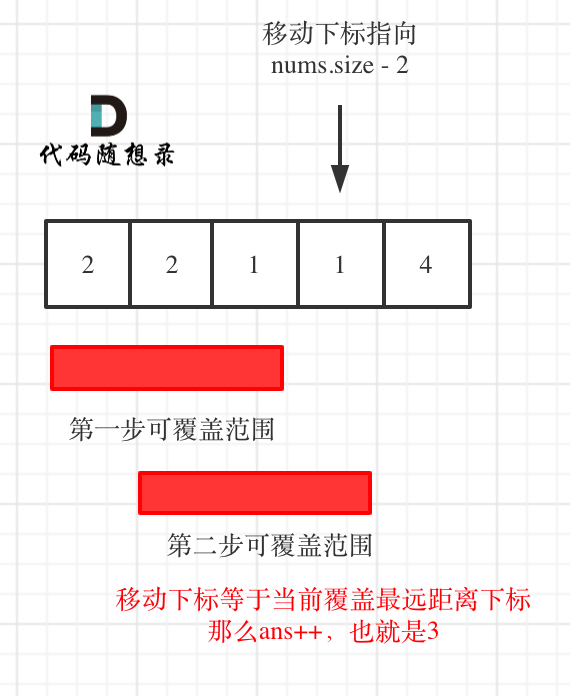
想要达到这样的效果，只要让移动下标，最大只能移动到 nums.size - 2 的地方就可以了。

因为当移动下标指向 nums.size - 2 时：

  • 如果移动下标等于当前覆盖最大距离下标， 需要再走一步（即 ans++），因为最后一步一定是可以到的终点。（题目假设总是可以到达数组的最后一个位置），如图： 45.跳跃游戏II2

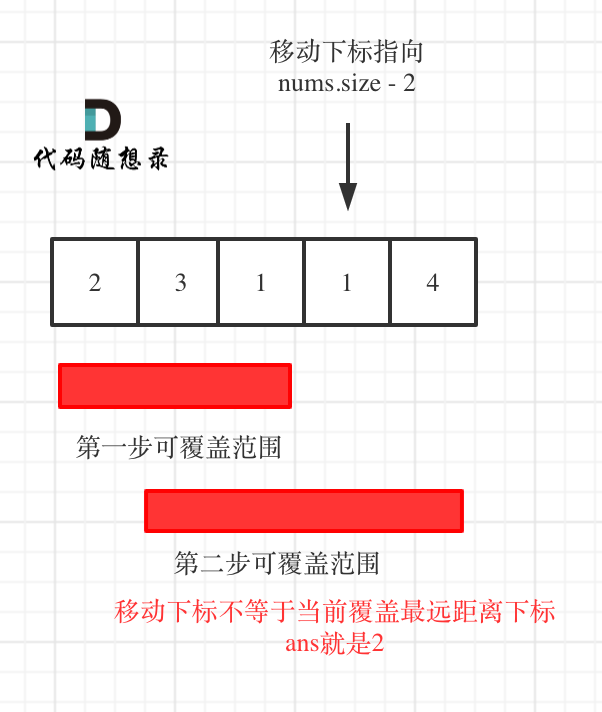
  • 如果移动下标不等于当前覆盖最大距离下标，说明当前覆盖最远距离就可以直接达到终点了，不需要再走一步。如图：

45.跳跃游戏II1

代码如下：

// 版本二
class Solution {
public:
    int jump(vector<int>& nums) {
        int curDistance = 0;    // 当前覆盖的最远距离下标
        int ans = 0;            // 记录走的最大步数
        int nextDistance = 0;   // 下一步覆盖的最远距离下标
        for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1，这是关键所在
            nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
            if (i == curDistance) {                 // 遇到当前覆盖的最远距离下标
                curDistance = nextDistance;         // 更新当前覆盖的最远距离下标
                ans++;
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
  • 时间复杂度: O(n)
  • 空间复杂度: O(1)

可以看出版本二的代码相对于版本一简化了不少！

其精髓在于控制移动下标 i 只移动到 nums.size() - 2 的位置，所以移动下标只要遇到当前覆盖最远距离的下标，直接步数加一，不用考虑别的了。

# 总结

相信大家可以发现，这道题目相当于55.跳跃游戏 (opens new window)难了不止一点。

但代码又十分简单，贪心就是这么巧妙。

理解本题的关键在于：以最小的步数增加最大的覆盖范围，直到覆盖范围覆盖了终点，这个范围内最少步数一定可以跳到，不用管具体是怎么跳的，不纠结于一步究竟跳一个单位还是两个单位。

# 其他语言版本

# Java

// 版本一
class Solution {
    public int jump(int[] nums) {
        if (nums == null || nums.length == 0 || nums.length == 1) {
            return 0;
        }
        //记录跳跃的次数
        int count=0;
        //当前的覆盖最大区域
        int curDistance = 0;
        //最大的覆盖区域
        int maxDistance = 0;
        for (int i = 0; i < nums.length; i++) {
            //在可覆盖区域内更新最大的覆盖区域
            maxDistance = Math.max(maxDistance,i+nums[i]);
            //说明当前一步，再跳一步就到达了末尾
            if (maxDistance>=nums.length-1){
                count++;
                break;
            }
            //走到当前覆盖的最大区域时，更新下一步可达的最大区域
            if (i==curDistance){
                curDistance = maxDistance;
                count++;
            }
        }
        return count;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 版本二
class Solution {
    public int jump(int[] nums) {
        int result = 0;
        // 当前覆盖的最远距离下标
        int end = 0;
        // 下一步覆盖的最远距离下标
        int temp = 0;
        for (int i = 0; i <= end && end < nums.length - 1; ++i) {
            temp = Math.max(temp, i + nums[i]);
            // 可达位置的改变次数就是跳跃次数
            if (i == end) {
                end = temp;
                result++;
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# Python

贪心（版本一）

class Solution:
    def jump(self, nums):
        if len(nums) == 1:
            return 0
        
        cur_distance = 0  # 当前覆盖最远距离下标
        ans = 0  # 记录走的最大步数
        next_distance = 0  # 下一步覆盖最远距离下标
        
        for i in range(len(nums)):
            next_distance = max(nums[i] + i, next_distance)  # 更新下一步覆盖最远距离下标
            if i == cur_distance:  # 遇到当前覆盖最远距离下标
                ans += 1  # 需要走下一步
                cur_distance = next_distance  # 更新当前覆盖最远距离下标（相当于加油了）
                if next_distance >= len(nums) - 1:  # 当前覆盖最远距离达到数组末尾，不用再做ans++操作，直接结束
                    break
        
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

贪心（版本二）

class Solution:
    def jump(self, nums):
        cur_distance = 0  # 当前覆盖的最远距离下标
        ans = 0  # 记录走的最大步数
        next_distance = 0  # 下一步覆盖的最远距离下标
        
        for i in range(len(nums) - 1):  # 注意这里是小于len(nums) - 1，这是关键所在
            next_distance = max(nums[i] + i, next_distance)  # 更新下一步覆盖的最远距离下标
            if i == cur_distance:  # 遇到当前覆盖的最远距离下标
                cur_distance = next_distance  # 更新当前覆盖的最远距离下标
                ans += 1
        
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14

贪心（版本三） 类似‘55-跳跃游戏’写法

class Solution:
    def jump(self, nums) -> int:
        if len(nums)==1:  # 如果数组只有一个元素，不需要跳跃，步数为0
            return 0
        
        i = 0  # 当前位置
        count = 0  # 步数计数器
        cover = 0  # 当前能够覆盖的最远距离
        
        while i <= cover:  # 当前位置小于等于当前能够覆盖的最远距离时循环
            for i in range(i, cover+1):  # 遍历从当前位置到当前能够覆盖的最远距离之间的所有位置
                cover = max(nums[i]+i, cover)  # 更新当前能够覆盖的最远距离
                if cover >= len(nums)-1:  # 如果当前能够覆盖的最远距离达到或超过数组的最后一个位置，直接返回步数+1
                    return count+1
            count += 1  # 每一轮遍历结束后，步数+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

动态规划

class Solution:
    def jump(self, nums: List[int]) -> int:
        result = [10**4+1] * len(nums)  # 初始化结果数组，初始值为一个较大的数
        result[0] = 0  # 起始位置的步数为0

        for i in range(len(nums)):  # 遍历数组
            for j in range(nums[i] + 1):  # 在当前位置能够跳跃的范围内遍历
                if i + j < len(nums):  # 确保下一跳的位置不超过数组范围
                    result[i + j] = min(result[i + j], result[i] + 1)  # 更新到达下一跳位置的最少步数

        return result[-1]  # 返回到达最后一个位置的最少步数
1
2
3
4
5
6
7
8
9
10
11
12
13

# Go

/**
 * @date: 2024 Jan 06
 * @time: 13:44
 * @author: Chris
**/
// 贪心算法优化版

// 记录步骤规则：每超过上一次可达最大范围，需要跳跃一次，次数+1
// 记录位置：i == lastDistance + 1
func jump(nums []int) int {
	// 根据题目规则，初始位置为nums[0]
	lastDistance := 0 // 上一次覆盖范围
	curDistance := 0  // 当前覆盖范围（可达最大范围）
	minStep := 0      // 记录最少跳跃次数

	for i := 0; i < len(nums); i++ {
		if i == lastDistance+1 { // 在上一次可达范围+1的位置，记录步骤
			minStep++                  // 跳跃次数+1
			lastDistance = curDistance // 记录时才可以更新
		}
		curDistance = max(nums[i]+i, curDistance) // 更新当前可达的最大范围
	}
	return minStep
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 贪心版本一
func jump(nums []int) int {
    n := len(nums)
    if n == 1 {
        return 0
    }
    cur, next := 0, 0
    step := 0
    for i := 0; i < n; i++ {
        next = max(nums[i]+i, next)
        if i == cur {
            if cur != n-1 {
                step++
                cur = next
                if cur >= n-1 {
                    return step
                }
            } else {
                return step
            }
        }
    }
    return step
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 贪心版本二
func jump(nums []int) int {
    n := len(nums)
    if n == 1 {
        return 0
    }
    cur, next := 0, 0
    step := 0
    for i := 0; i < n-1; i++ {
        next = max(nums[i]+i, next)
        if i == cur {
            cur = next
            step++
        }
    }
    return step
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# Javascript

var jump = function(nums) {
    let curIndex = 0
    let nextIndex = 0
    let steps = 0
    for(let i = 0; i < nums.length - 1; i++) {
        nextIndex = Math.max(nums[i] + i, nextIndex)
        if(i === curIndex) {
            curIndex = nextIndex
            steps++
        }
    }

    return steps
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# TypeScript

function jump(nums: number[]): number {
  const length: number = nums.length;
  let curFarthestIndex: number = 0,
    nextFarthestIndex: number = 0;
  let curIndex: number = 0;
  let stepNum: number = 0;
  while (curIndex < length - 1) {
    nextFarthestIndex = Math.max(nextFarthestIndex, curIndex + nums[curIndex]);
    if (curIndex === curFarthestIndex) {
      curFarthestIndex = nextFarthestIndex;
      stepNum++;
    }
    curIndex++;
  }
  return stepNum;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# Scala

object Solution {
  def jump(nums: Array[Int]): Int = {
    if (nums.length == 0) return 0
    var result = 0 // 记录走的最大步数
    var curDistance = 0 // 当前覆盖最远距离下标
    var nextDistance = 0 // 下一步覆盖最远距离下标
    for (i <- nums.indices) {
      nextDistance = math.max(nums(i) + i, nextDistance) // 更新下一步覆盖最远距离下标
      if (i == curDistance) {
        if (curDistance != nums.length - 1) {
          result += 1
          curDistance = nextDistance
          if (nextDistance >= nums.length - 1) return result
        } else {
          return result
        }
      }
    }
    result
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# Rust

//版本一
impl Solution {
    pub fn jump(nums: Vec<i32>) -> i32 {
        if nums.len() == 1 {
            return 0;
        }
        let mut cur_distance = 0;
        let mut ans = 0;
        let mut next_distance = 0;
        for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
            next_distance = (n as usize + i).max(next_distance);
            if i == cur_distance {
                if cur_distance < nums.len() - 1 {
                    ans += 1;
                    cur_distance = next_distance;
                    if next_distance >= nums.len() - 1 {
                        break;
                    };
                } else {
                    break;
                }
            }
        }
        ans
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//版本二
impl Solution {
    pub fn jump(nums: Vec<i32>) -> i32 {
        if nums.len() == 1 {
            return 0;
        }
        let mut cur_distance = 0;
        let mut ans = 0;
        let mut next_distance = 0;
        for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
            next_distance = (n as usize + i).max(next_distance);
            if i == cur_distance {
                cur_distance = next_distance;
                ans += 1;
            }
        }
        ans
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# C

#define max(a, b) ((a) > (b) ? (a) : (b))

int jump(int* nums, int numsSize) {
    if(numsSize == 1){
        return 0;
    }
    int count = 0;
    // 记录当前能走的最远距离
    int curDistance = 0;
    // 记录下一步能走的最远距离
    int nextDistance = 0;
    for(int i = 0; i < numsSize; i++){
        nextDistance = max(i + nums[i], nextDistance);
        // 下标到了当前的最大距离
        if(i == nextDistance){
            count++;
            curDistance = nextDistance;
        }
    }
    return count;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# C#

// 版本二
public class Solution
{
    public int Jump(int[] nums)
    {
        int cur = 0, next = 0, step = 0;
        for (int i = 0; i < nums.Length - 1; i++)
        {
            next = Math.Max(next, i + nums[i]);
            if (i == cur)
            {
                cur = next;
                step++;
            }
        }
        return step;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
上次更新：: 8/22/2024, 9:07:28 PM

← 9. K次取反后最大化的数组和 →

@2021-2024 代码随想录 版权所有 粤ICP备19156078号