参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

用队列实现栈还是有点别扭。

225. 用队列实现栈

力扣题目链接 (opens new window)

使用队列实现栈的下列操作：

• push(x) -- 元素 x 入栈
• pop() -- 移除栈顶元素
• top() -- 获取栈顶元素
• empty() -- 返回栈是否为空

注意:

• 你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
• 你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。
• 你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。

算法公开课

《代码随想录》算法视频公开课 (opens new window)：队列的基本操作！ | LeetCode：225. 用队列实现栈 (opens new window)，相信结合视频再看本篇题解，更有助于大家对本题的理解。

思路

（这里要强调是单向队列）

有的同学可能疑惑这种题目有什么实际工程意义，其实很多算法题目主要是对知识点的考察和教学意义远大于其工程实践的意义，所以面试题也是这样！

刚刚做过栈与队列：我用栈来实现队列怎么样？ (opens new window)的同学可能依然想着用一个输入队列，一个输出队列，就可以模拟栈的功能，仔细想一下还真不行！

队列模拟栈，其实一个队列就够了，那么我们先说一说两个队列来实现栈的思路。

队列是先进先出的规则，把一个队列中的数据导入另一个队列中，数据的顺序并没有变，并没有变成先进后出的顺序。

所以用栈实现队列， 和用队列实现栈的思路还是不一样的，这取决于这两个数据结构的性质。

但是依然还是要用两个队列来模拟栈，只不过没有输入和输出的关系，而是另一个队列完全用来备份的！

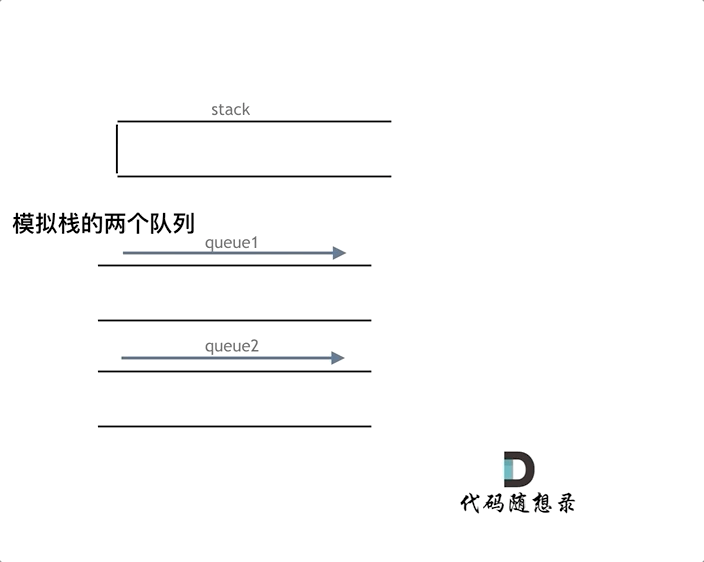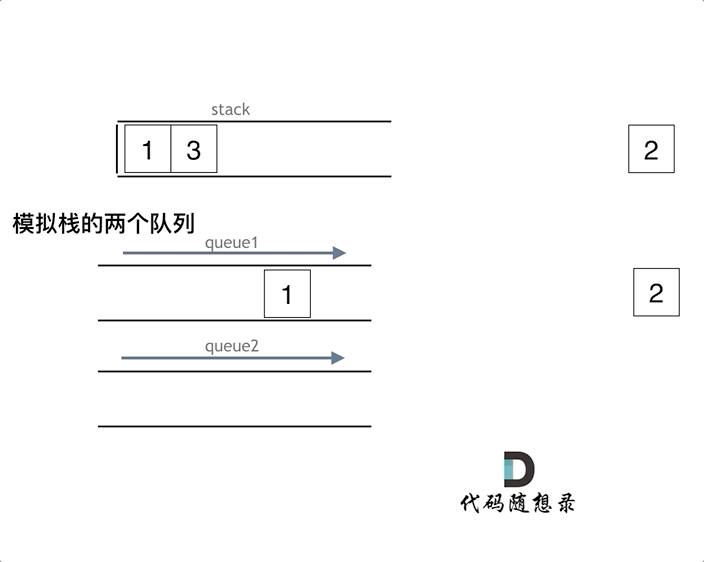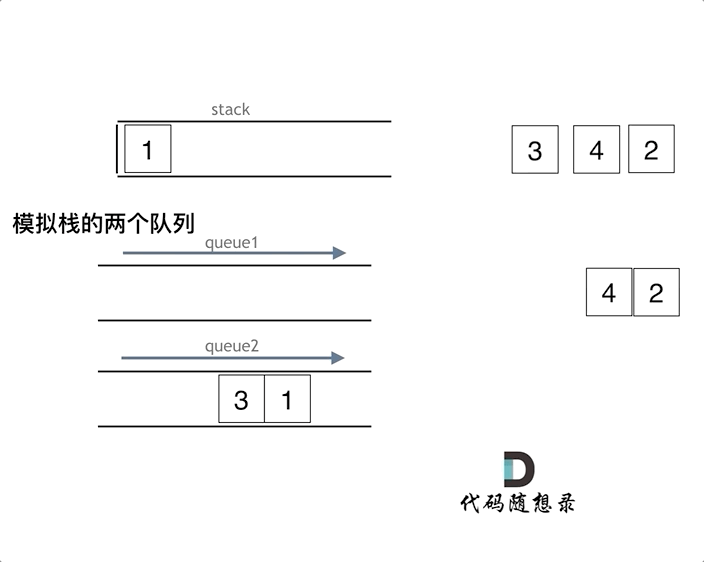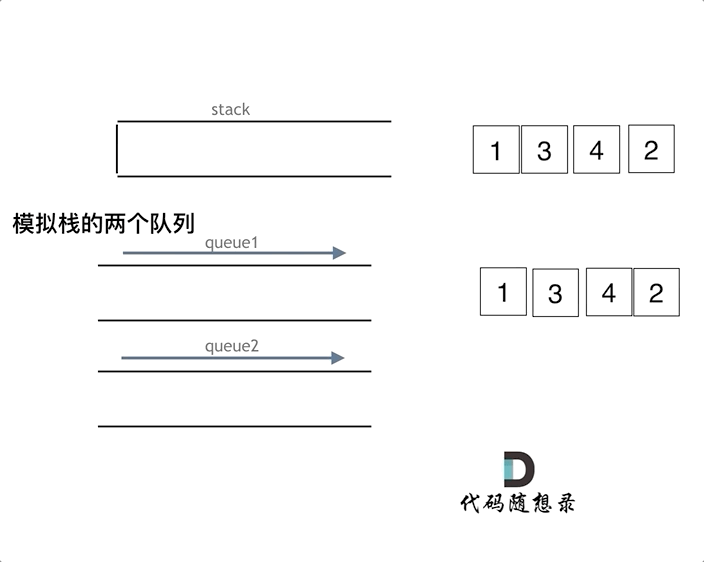
如下面动画所示，用两个队列que1和que2实现队列的功能，que2其实完全就是一个备份的作用，把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1。

模拟的队列执行语句如下：

queue.push(1);        
queue.push(2);        
queue.pop();   // 注意弹出的操作       
queue.push(3);        
queue.push(4);       
queue.pop();  // 注意弹出的操作    
queue.pop();    
queue.pop();    
queue.empty();    

详细如代码注释所示：

class MyStack {
public:
    queue<int> que1;
    queue<int> que2; // 辅助队列，用来备份

    /** Initialize your data structure here. */
    MyStack() {

    }

    /** Push element x onto stack. */
    void push(int x) {
        que1.push(x);
    }

    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int size = que1.size();
        size--;
        while (size--) { // 将que1 导入que2，但要留下最后一个元素
            que2.push(que1.front());
            que1.pop();
        }

        int result = que1.front(); // 留下的最后一个元素就是要返回的值
        que1.pop();
        que1 = que2;            // 再将que2赋值给que1
        while (!que2.empty()) { // 清空que2
            que2.pop();
        }
        return result;
    }

    /** Get the top element.
     ** Can not use back() direactly.
     */
    int top(){
        int size = que1.size();
        size--;
        while (size--){
            // 将que1 导入que2，但要留下最后一个元素
            que2.push(que1.front());
            que1.pop();
        }

        int result = que1.front(); // 留下的最后一个元素就是要回返的值
        que2.push(que1.front());   // 获取值后将最后一个元素也加入que2中，保持原本的结构不变
        que1.pop();

        que1 = que2; // 再将que2赋值给que1
        while (!que2.empty()){
            // 清空que2
            que2.pop();
        }
        return result;
    }

    /** Returns whether the stack is empty. */
    bool empty() {
        return que1.empty();
    }
};

• 时间复杂度: pop为O(n)，top为O(n)，其他为O(1)
• 空间复杂度: O(n)

优化

其实这道题目就是用一个队列就够了。

一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。

C++优化代码

class MyStack {
public:
    queue<int> que;

    MyStack() {

    }

    void push(int x) {
        que.push(x);
    }

    int pop() {
        int size = que.size();
        size--;
        while (size--) { // 将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部
            que.push(que.front());
            que.pop();
        }
        int result = que.front(); // 此时弹出的元素顺序就是栈的顺序了
        que.pop();
        return result;
    }

    int top(){
        int size = que.size();
        size--;
        while (size--){
            // 将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部
            que.push(que.front());
            que.pop();
        }
        int result = que.front(); // 此时获得的元素就是栈顶的元素了
        que.push(que.front());    // 将获取完的元素也重新添加到队列尾部，保证数据结构没有变化
        que.pop();
        return result;
    }

    bool empty() {
        return que.empty();
    }
};

• 时间复杂度: pop为O(n)，top为O(n)，其他为O(1)
• 空间复杂度: O(n)

其他语言版本

Java：

使用两个 Queue 实现方法1

class MyStack {

    Queue<Integer> queue1; // 和栈中保持一样元素的队列
    Queue<Integer> queue2; // 辅助队列

    /** Initialize your data structure here. */
    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        queue2.offer(x); // 先放在辅助队列中
        while (!queue1.isEmpty()){
            queue2.offer(queue1.poll());
        }
        Queue<Integer> queueTemp;
        queueTemp = queue1;
        queue1 = queue2;
        queue2 = queueTemp; // 最后交换queue1和queue2，将元素都放到queue1中
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue1.poll(); // 因为queue1中的元素和栈中的保持一致，所以这个和下面两个的操作只看queue1即可
    }
    
    /** Get the top element. */
    public int top() {
        return queue1.peek();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue1.isEmpty();
    }
}

使用两个 Queue 实现方法2

class MyStack {
    //q1作为主要的队列，其元素排列顺序和出栈顺序相同
    Queue<Integer> q1 = new ArrayDeque<>();
    //q2仅作为临时放置
    Queue<Integer> q2 = new ArrayDeque<>();

    public MyStack() {

    }
    //在加入元素时先将q1中的元素依次出栈压入q2，然后将新加入的元素压入q1，再将q2中的元素依次出栈压入q1
    public void push(int x) {
        while (q1.size() > 0) {
            q2.add(q1.poll());
        }
        q1.add(x);
        while (q2.size() > 0) {
            q1.add(q2.poll());
        }
    }

    public int pop() {
        return q1.poll();
    }

    public int top() {
        return q1.peek();
    }

    public boolean empty() {
        return q1.isEmpty();
    }
}

使用两个 Deque 实现

class MyStack {
    // Deque 接口继承了 Queue 接口
    // 所以 Queue 中的 add、poll、peek等效于 Deque 中的 addLast、pollFirst、peekFirst
    Deque<Integer> que1; // 和栈中保持一样元素的队列
    Deque<Integer> que2; // 辅助队列
    /** Initialize your data structure here. */
    public MyStack() {
        que1 = new ArrayDeque<>();
        que2 = new ArrayDeque<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        que1.addLast(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        int size = que1.size();
        size--;
        // 将 que1 导入 que2 ，但留下最后一个值
        while (size-- > 0) {
            que2.addLast(que1.peekFirst());
            que1.pollFirst();
        }

        int res = que1.pollFirst();
        // 将 que2 对象的引用赋给了 que1 ，此时 que1，que2 指向同一个队列
        que1 = que2;
        // 如果直接操作 que2，que1 也会受到影响，所以为 que2 分配一个新的空间
        que2 = new ArrayDeque<>();
        return res;
    }
    
    /** Get the top element. */
    public int top() {
        return que1.peekLast();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return que1.isEmpty();
    }
}

优化，使用一个 Deque 实现

class MyStack {
    // Deque 接口继承了 Queue 接口
    // 所以 Queue 中的 add、poll、peek等效于 Deque 中的 addLast、pollFirst、peekFirst
    Deque<Integer> que1;
    /** Initialize your data structure here. */
    public MyStack() {
        que1 = new ArrayDeque<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        que1.addLast(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        int size = que1.size();
        size--;
        // 将 que1 导入 que2 ，但留下最后一个值
        while (size-- > 0) {
            que1.addLast(que1.peekFirst());
            que1.pollFirst();
        }

        int res = que1.pollFirst();
        return res;
    }
    
    /** Get the top element. */
    public int top() {
        return que1.peekLast();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return que1.isEmpty();
    }
}

优化，使用一个 Queue 实现

class MyStack {

    Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<>();
    }

    //每 offer 一个数（A）进来，都重新排列，把这个数（A）放到队列的队首
    public void push(int x) {
        queue.offer(x);
        int size = queue.size();
        //移动除了 A 的其它数
        while (size-- > 1)
            queue.offer(queue.poll());
    }

    public int pop() {
        return queue.poll();
    }

    public int top() {
        return queue.peek();
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

优化，使用一个 Queue 实现，但用卡哥的逻辑实现

class MyStack {
    Queue<Integer> queue;
    
    public MyStack() {
        queue = new LinkedList<>();
    }
    
    public void push(int x) {
        queue.add(x);
    }
    
    public int pop() {
        rePosition();
        return queue.poll();
    }
    
    public int top() {
        rePosition();
        int result = queue.poll();
        queue.add(result);
        return result;
    }
    
    public boolean empty() {
        return queue.isEmpty();
    }

    public void rePosition(){
        int size = queue.size();
        size--;
        while(size-->0)
            queue.add(queue.poll());
    }
}

Python：

from collections import deque

class MyStack:

    def __init__(self):
        """
        Python普通的Queue或SimpleQueue没有类似于peek的功能
        也无法用索引访问，在实现top的时候较为困难。

        用list可以，但是在使用pop(0)的时候时间复杂度为O(n)
        因此这里使用双向队列，我们保证只执行popleft()和append()，因为deque可以用索引访问，可以实现和peek相似的功能

        in - 存所有数据
        out - 仅在pop的时候会用到
        """
        self.queue_in = deque()
        self.queue_out = deque()

    def push(self, x: int) -> None:
        """
        直接append即可
        """
        self.queue_in.append(x)


    def pop(self) -> int:
        """
        1. 首先确认不空
        2. 因为队列的特殊性，FIFO，所以我们只有在pop()的时候才会使用queue_out
        3. 先把queue_in中的所有元素（除了最后一个），依次出列放进queue_out
        4. 交换in和out，此时out里只有一个元素
        5. 把out中的pop出来，即是原队列的最后一个
        
        tip：这不能像栈实现队列一样，因为另一个queue也是FIFO，如果执行pop()它不能像
        stack一样从另一个pop()，所以干脆in只用来存数据，pop()的时候两个进行交换
        """
        if self.empty():
            return None

        for i in range(len(self.queue_in) - 1):
            self.queue_out.append(self.queue_in.popleft())
        
        self.queue_in, self.queue_out = self.queue_out, self.queue_in    # 交换in和out，这也是为啥in只用来存
        return self.queue_out.popleft()

    def top(self) -> int:
        """
        写法一：
        1. 首先确认不空
        2. 我们仅有in会存放数据，所以返回第一个即可（这里实际上用到了栈）
        写法二：
        1. 首先确认不空
        2. 因为队列的特殊性，FIFO，所以我们只有在pop()的时候才会使用queue_out
        3. 先把queue_in中的所有元素（除了最后一个），依次出列放进queue_out
        4. 交换in和out，此时out里只有一个元素
        5. 把out中的pop出来，即是原队列的最后一个，并使用temp变量暂存
        6. 把temp追加到queue_in的末尾
        """
        # 写法一：
        # if self.empty():
        #     return None
        
        # return self.queue_in[-1]    # 这里实际上用到了栈，因为直接获取了queue_in的末尾元素

        # 写法二：
        if self.empty():
            return None

        for i in range(len(self.queue_in) - 1):
            self.queue_out.append(self.queue_in.popleft())
        
        self.queue_in, self.queue_out = self.queue_out, self.queue_in 
        temp = self.queue_out.popleft()   
        self.queue_in.append(temp)
        return temp


    def empty(self) -> bool:
        """
        因为只有in存了数据，只要判断in是不是有数即可
        """
        return len(self.queue_in) == 0

优化，使用一个队列实现

class MyStack:

    def __init__(self):
        self.que = deque()

    def push(self, x: int) -> None:
        self.que.append(x)

    def pop(self) -> int:
        if self.empty():
            return None
        for i in range(len(self.que)-1):
            self.que.append(self.que.popleft())
        return self.que.popleft()

    def top(self) -> int:
        # 写法一：
        # if self.empty():
        #     return None
        # return self.que[-1]

        # 写法二：
        if self.empty():
            return None
        for i in range(len(self.que)-1):
            self.que.append(self.que.popleft())
        temp = self.que.popleft()
        self.que.append(temp)
        return temp

    def empty(self) -> bool:
        return not self.que

Go：

使用两个队列实现

type MyStack struct {
    //创建两个队列
    queue1 []int
    queue2 []int
}


func Constructor() MyStack {
    return MyStack{	//初始化
        queue1:make([]int,0),
        queue2:make([]int,0),
    }
}


func (this *MyStack) Push(x int)  {
     //先将数据存在queue2中
    this.queue2 = append(this.queue2,x)	
   //将queue1中所有元素移到queue2中，再将两个队列进行交换
    this.Move() 
}


func (this *MyStack) Move(){    
    if len(this.queue1) == 0{
        //交换，queue1置为queue2,queue2置为空
        this.queue1,this.queue2 = this.queue2,this.queue1
    }else{
        //queue1元素从头开始一个一个追加到queue2中
            this.queue2 = append(this.queue2,this.queue1[0])  
            this.queue1 = this.queue1[1:]	//去除第一个元素
            this.Move()     //重复
    }
}

func (this *MyStack) Pop() int {
    val := this.queue1[0]
    this.queue1 = this.queue1[1:]	//去除第一个元素
    return val

}


func (this *MyStack) Top() int {
    return this.queue1[0]	//直接返回
}


func (this *MyStack) Empty() bool {
return len(this.queue1) == 0
}


/**
 * Your MyStack object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Push(x);
 * param_2 := obj.Pop();
 * param_3 := obj.Top();
 * param_4 := obj.Empty();
 */

使用一个队列实现

type MyStack struct {
    queue []int//创建一个队列
}


/** Initialize your data structure here. */
func Constructor() MyStack {
    return MyStack{   //初始化
        queue:make([]int,0),
    }
}


/** Push element x onto stack. */
func (this *MyStack) Push(x int)  {
    //添加元素
    this.queue=append(this.queue,x)
}


/** Removes the element on top of the stack and returns that element. */
func (this *MyStack) Pop() int {
    n:=len(this.queue)-1//判断长度
    for n!=0{ //除了最后一个，其余的都重新添加到队列里
        val:=this.queue[0]
        this.queue=this.queue[1:]
        this.queue=append(this.queue,val)
        n--
    }
    //弹出元素
    val:=this.queue[0]
    this.queue=this.queue[1:]
    return val
    
}


/** Get the top element. */
func (this *MyStack) Top() int {
    //利用Pop函数，弹出来的元素重新添加
    val:=this.Pop()
    this.queue=append(this.queue,val)
    return val
}


/** Returns whether the stack is empty. */
func (this *MyStack) Empty() bool {
    return len(this.queue)==0
}


/**
 * Your MyStack object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Push(x);
 * param_2 := obj.Pop();
 * param_3 := obj.Top();
 * param_4 := obj.Empty();
 */

JavaScript:

使用数组（push, shift）模拟队列

// 使用两个队列实现
/**
 * Initialize your data structure here.
 */
var MyStack = function() {
    this.queue1 = [];
    this.queue2 = [];
};

/**
 * Push element x onto stack. 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queue1.push(x);
};

/**
 * Removes the element on top of the stack and returns that element.
 * @return {number}
 */
MyStack.prototype.pop = function() {
    // 减少两个队列交换的次数， 只有当queue1为空时，交换两个队列
    if(!this.queue1.length) {
        [this.queue1, this.queue2] = [this.queue2, this.queue1];
    }
    while(this.queue1.length > 1) {
        this.queue2.push(this.queue1.shift());
    }
    return this.queue1.shift();
};

/**
 * Get the top element.
 * @return {number}
 */
MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue1.push(x);
    return x;
};

/**
 * Returns whether the stack is empty.
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return !this.queue1.length && !this.queue2.length;
};

// 使用一个队列实现
/**
 * Initialize your data structure here.
 */
var MyStack = function() {
    this.queue = [];
};

/**
 * Push element x onto stack. 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queue.push(x);
};

/**
 * Removes the element on top of the stack and returns that element.
 * @return {number}
 */
MyStack.prototype.pop = function() {
    let size = this.queue.length;
    while(size-- > 1) {
        this.queue.push(this.queue.shift());
    }
    return this.queue.shift();
};

/**
 * Get the top element.
 * @return {number}
 */
MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue.push(x);
    return x;
};

/**
 * Returns whether the stack is empty.
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return !this.queue.length;
};

TypeScript:

版本一：使用两个队列模拟栈

class MyStack {
    private queue: number[];
    private tempQueue: number[];
    constructor() {
        this.queue = [];
        this.tempQueue = [];
    }

    push(x: number): void {
        this.queue.push(x);
    }

    pop(): number {
        for (let i = 0, length = this.queue.length - 1; i < length; i++) {
            this.tempQueue.push(this.queue.shift()!);
        }
        let res: number = this.queue.pop()!;
        let temp: number[] = this.queue;
        this.queue = this.tempQueue;
        this.tempQueue = temp;
        return res;
    }

    top(): number {
        let res: number = this.pop();
        this.push(res);
        return res;
    }

    empty(): boolean {
        return this.queue.length === 0;
    }
}

版本二：使用一个队列模拟栈

class MyStack {
    private queue: number[];
    constructor() {
        this.queue = [];
    }

    push(x: number): void {
        this.queue.push(x);
    }

    pop(): number {
        for (let i = 0, length = this.queue.length - 1; i < length; i++) {
            this.queue.push(this.queue.shift()!);
        }
        return this.queue.shift()!;
    }

    top(): number {
        let res: number = this.pop();
        this.push(res);
        return res;
    }

    empty(): boolean {
        return this.queue.length === 0;
    }
}

Swift:

// 定义一个队列数据结构
class Queue {
    var array: [Int]
    init() {
        array = [Int]()
    }
    
    /** Push element x to the back of queue. */
    func push(_ x: Int) {
        array.append(x)
    }
    
    /** Removes the element from in front of queue and returns that element. */
    func pop() -> Int {
        if array.isEmpty {
            return -1
        }
        return array.removeFirst()
    }
    
    /** Get the front element. */
    func peek() -> Int {
        if array.isEmpty {
            return -1
        }
        return array.first!
    }
    
    /** Returns whether the queue is empty. */
    func empty() -> Bool {
        return array.isEmpty
    }
    
    func count() -> Int {
        return array.count
    }
}

// 使用双队列
class MyStack {
    var queue1: Queue
    var queue2: Queue
    
    init() {
        queue1 = Queue()
        queue2 = Queue()
    }
    
    func push(_ x: Int) {
        queue1.push(x)
    }
    
    func pop() -> Int {
        if queue1.empty() {
            return -1
        }
        while queue1.count() > 1 {
            queue2.push(queue1.pop())
        }
        let res = queue1.pop()
        while !queue2.empty() {
            queue1.push(queue2.pop())
        }
        return res
    }
    
    func top() -> Int {
        if queue1.empty() {
            return -1
        }
        let res = pop()
        push(res)
        return res
    }
    
    func empty() -> Bool {
        return queue1.empty() && queue2.empty()
    }
}

// 使用单队列
class MyStack {
    var queue: Queue
    
    init() {
        queue = Queue()
    }
    
    func push(_ x: Int) {
        queue.push(x)
    }
    
    func pop() -> Int {
        if queue.empty() {
            return -1
        }
        for _ in 1 ..< queue.count() {
            queue.push(queue.pop())
        }
        return queue.pop()
    }
    
    func top() -> Int {
        if queue.empty() {
            return -1
        }
        let res = pop()
        push(res)
        return res
    }
    
    func empty() -> Bool {
        return queue.empty()
    }
}

Scala:

使用两个队列模拟栈:

import scala.collection.mutable

class MyStack() {

  val queue1 = new mutable.Queue[Int]()
  val queue2 = new mutable.Queue[Int]()

  def push(x: Int) {
    queue1.enqueue(x)
  }

  def pop(): Int = {
    var size = queue1.size
    // 将queue1中的每个元素都移动到queue2
    for (i <- 0 until size - 1) {
      queue2.enqueue(queue1.dequeue())
    }
    var res = queue1.dequeue()
    // 再将queue2中的每个元素都移动到queue1
    while (!queue2.isEmpty) {
      queue1.enqueue(queue2.dequeue())
    }
    res
  }

  def top(): Int = {
    var size = queue1.size
    for (i <- 0 until size - 1) {
      queue2.enqueue(queue1.dequeue())
    }
    var res = queue1.dequeue()
    while (!queue2.isEmpty) {
      queue1.enqueue(queue2.dequeue())
    }
    // 最终还需要把res送进queue1
    queue1.enqueue(res)
    res
  }

  def empty(): Boolean = {
    queue1.isEmpty
  }
}

使用一个队列模拟:

import scala.collection.mutable

class MyStack() {

  val queue = new mutable.Queue[Int]()

  def push(x: Int) {
    queue.enqueue(x)
  }

  def pop(): Int = {
    var size = queue.size
    for (i <- 0 until size - 1) {
      queue.enqueue(queue.head) // 把头添到队列最后
      queue.dequeue() // 再出队
    }
    queue.dequeue()
  }

  def top(): Int = {
    var size = queue.size
    var res = 0
    for (i <- 0 until size) {
      queue.enqueue(queue.head) // 把头添到队列最后
      res = queue.dequeue() // 再出队
    }
    res
  }

  def empty(): Boolean = {
    queue.isEmpty
  }
  }

C#:

双队列

public class MyStack {
    Queue<int> queue1;
    Queue<int> queue2;
    public MyStack() {
        queue1 = new Queue<int>();
        queue2 = new Queue<int>();
    }
    
    public void Push(int x) {
        queue2.Enqueue(x);
        while(queue1.Count != 0){
            queue2.Enqueue(queue1.Dequeue());
        }
        Queue<int> queueTemp;
        queueTemp = queue1;
        queue1 = queue2;
        queue2 = queueTemp;
    }
    
    public int Pop() {
        return queue1.Count > 0 ? queue1.Dequeue() : -1;
    }
    
    public int Top() {
        return queue1.Count > 0 ? queue1.Peek() : -1;
    }
    
    public bool Empty() {
        return queue1.Count == 0;
    }
}

单队列

/*
 * @lc app=leetcode id=225 lang=csharp
 * 版本二：单队列
 * [225] Implement Stack using Queues
 */

// @lc code=start
public class MyStack {
    Queue<int> myQueue;
    public MyStack() {
        myQueue = new Queue<int>();
    }
    
    public void Push(int x) {
        myQueue.Enqueue(x);
    }
    
    //使用一个队列实现
    public int Pop() {
        //一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。
        for (var i = 0; i < myQueue.Count-1; i++)
        {
            myQueue.Enqueue(myQueue.Dequeue());
        }
        return myQueue.Dequeue();
    }

    //复用Pop()的代码
    public int Top() {
        int res = Pop();
        myQueue.Enqueue(res);
        return res;
    }
    
    public bool Empty() {
        return (myQueue.Count == 0);
    }
}

// @lc code=end

PHP:

双队列

// SplQueue 类通过使用一个双向链表来提供队列的主要功能。(PHP 5 >= 5.3.0, PHP 7, PHP 8)
// https://www.php.net/manual/zh/class.splqueue.php
class MyStack {
    public $queueMain; // 保存数据
    public $queueTmp;  // 辅助作用

    function __construct() {
        $this->queueMain=new SplQueue();
        $this->queueTmp=new SplQueue();
    }
    
    // queueMain: 1,2,3 <= add
    function push($x) {
        $this->queueMain->enqueue($x);
    }
                                    
    function pop() {
       $qmSize = $this->queueMain->Count();
       $qmSize --;
       // queueMain: 3,2,1 => pop =>2,1 => add => 2,1 :queueTmp
       while($qmSize --){
           $this->queueTmp->enqueue($this->queueMain->dequeue());
       }
       // queueMain: 3
       $val = $this->queueMain->dequeue();
       // queueMain <= queueTmp 
       $this->queueMain = $this->queueTmp;
       // 清空queueTmp,下次使用 
       $this->queueTmp = new SplQueue();
       return $val;
    }

    function top() {
        // 底层是双链表实现：从双链表的末尾查看节点
        return $this->queueMain->top(); 
    }

    function empty() {
        return $this->queueMain->isEmpty();
    }
}

单队列

class MyStack {
    public $queue;

    function __construct() {
        $this->queue=new SplQueue();
    }
    
    function push($x) {
        $this->queue->enqueue($x);
    }
                                 
    function pop() {
       $qmSize = $this->queue->Count();
       $qmSize --;
       //queue: 3,2,1 => pop =>2,1 => add => 2,1,3 :queue
       while($qmSize --){
           $this->queue->enqueue($this->queue->dequeue());
       }
       $val = $this->queue->dequeue();
       return $val;
    }

    function top() {
        return $this->queue->top(); 
    }

    function empty() {
        return $this->queue->isEmpty();
    }
}

Rust:

rust：单队列

struct MyStack {
    queue: Vec<i32>,
}

impl MyStack {
    fn new() -> Self {
        MyStack { queue: vec![] }
    }

    fn push(&mut self, x: i32) {
        self.queue.push(x);
    }

    fn pop(&mut self) -> i32 {
        let len = self.queue.len() - 1;
        for _ in 0..len {
            let tmp = self.queue.remove(0);
            self.queue.push(tmp);
        }
        self.queue.remove(0)
    }

    fn top(&mut self) -> i32 {
        let res = self.pop();
        self.queue.push(res);
        res
    }

    fn empty(&self) -> bool {
        self.queue.is_empty()
    }
}