参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

工作上一定没人这么搞，但是考察对栈、队列理解程度的好题

232.用栈实现队列

力扣题目链接 (opens new window)

使用栈实现队列的下列操作：

push(x) -- 将一个元素放入队列的尾部。
pop() -- 从队列首部移除元素。
peek() -- 返回队列首部的元素。
empty() -- 返回队列是否为空。

示例:

MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek();  // 返回 1
queue.pop();   // 返回 1
queue.empty(); // 返回 false

说明:

• 你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
• 假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）。

算法公开课

《代码随想录》算法视频公开课 (opens new window)：栈的基本操作！ | LeetCode：232.用栈实现队列 (opens new window)，相信结合视频再看本篇题解，更有助于大家对本题的理解。

思路

这是一道模拟题，不涉及到具体算法，考察的就是对栈和队列的掌握程度。

使用栈来模拟队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系。

下面动画模拟以下队列的执行过程：

执行语句：
queue.push(1);
queue.push(2);
queue.pop(); 注意此时的输出栈的操作
queue.push(3);
queue.push(4);
queue.pop();
queue.pop();注意此时的输出栈的操作
queue.pop();
queue.empty();

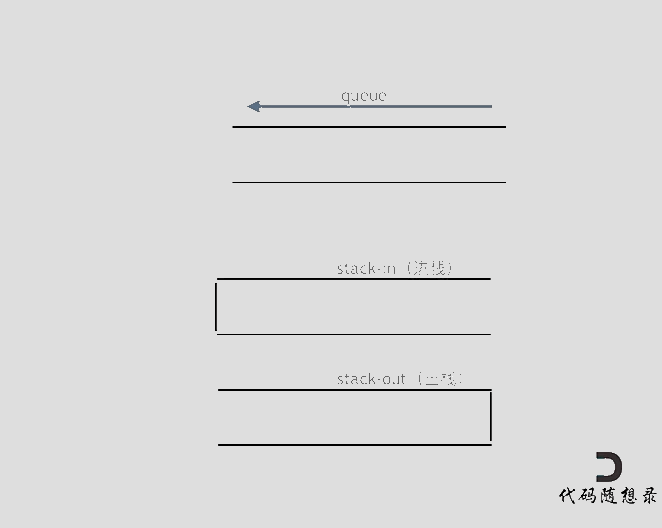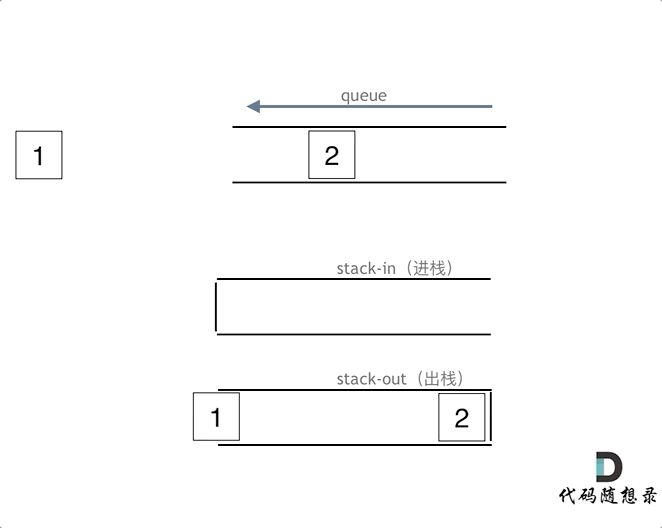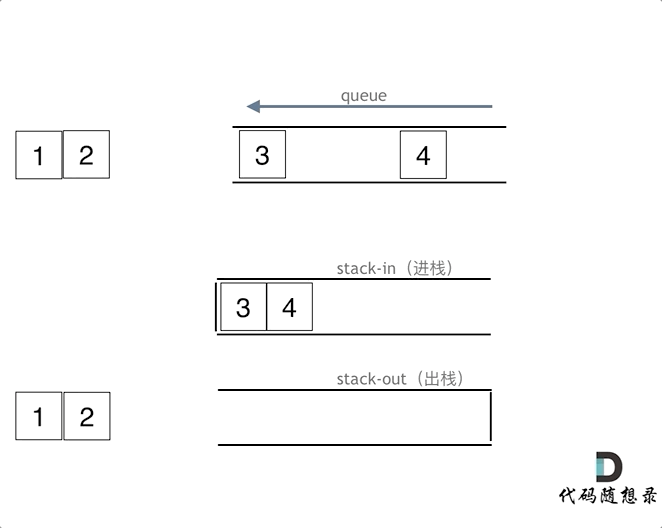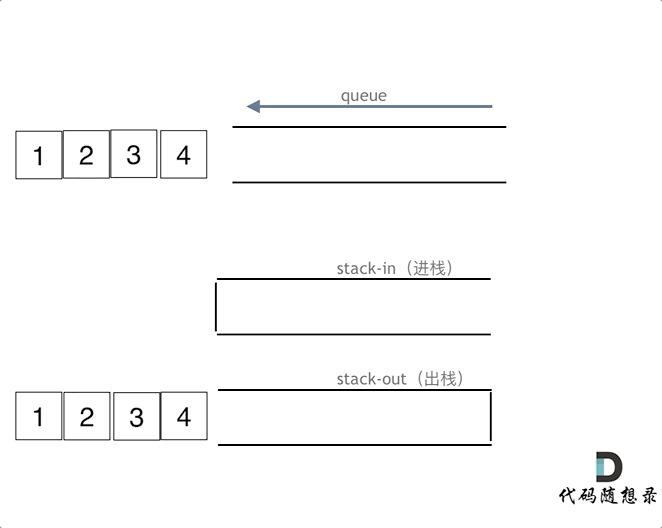
在push数据的时候，只要数据放进输入栈就好，但在pop的时候，操作就复杂一些，输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入），再从出栈弹出数据，如果输出栈不为空，则直接从出栈弹出数据就可以了。

最后如何判断队列为空呢？如果进栈和出栈都为空的话，说明模拟的队列为空了。

在代码实现的时候，会发现pop() 和 peek()两个函数功能类似，代码实现上也是类似的，可以思考一下如何把代码抽象一下。

C++代码如下：

class MyQueue {
public:
    stack<int> stIn;
    stack<int> stOut;
    /** Initialize your data structure here. */
    MyQueue() {

    }
    /** Push element x to the back of queue. */
    void push(int x) {
        stIn.push(x);
    }

    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        // 只有当stOut为空的时候，再从stIn里导入数据（导入stIn全部数据）
        if (stOut.empty()) {
            // 从stIn导入数据直到stIn为空
            while(!stIn.empty()) {
                stOut.push(stIn.top());
                stIn.pop();
            }
        }
        int result = stOut.top();
        stOut.pop();
        return result;
    }

    /** Get the front element. */
    int peek() {
        int res = this->pop(); // 直接使用已有的pop函数
        stOut.push(res); // 因为pop函数弹出了元素res，所以再添加回去
        return res;
    }

    /** Returns whether the queue is empty. */
    bool empty() {
        return stIn.empty() && stOut.empty();
    }
};

• 时间复杂度: push和empty为O(1), pop和peek为O(n)
• 空间复杂度: O(n)

拓展

可以看出peek()的实现，直接复用了pop()， 要不然，对stOut判空的逻辑又要重写一遍。

再多说一些代码开发上的习惯问题，在工业级别代码开发中，最忌讳的就是 实现一个类似的函数，直接把代码粘过来改一改就完事了。

这样的项目代码会越来越乱，一定要懂得复用，功能相近的函数要抽象出来，不要大量的复制粘贴，很容易出问题！（踩过坑的人自然懂）

工作中如果发现某一个功能自己要经常用，同事们可能也会用到，自己就花点时间把这个功能抽象成一个好用的函数或者工具类，不仅自己方便，也方便了同事们。

同事们就会逐渐认可你的工作态度和工作能力，自己的口碑都是这么一点一点积累起来的！在同事圈里口碑起来了之后，你就发现自己走上了一个正循环，以后的升职加薪才少不了你！

其他语言版本

Java：

class MyQueue {

    Stack<Integer> stackIn;
    Stack<Integer> stackOut;

    /** Initialize your data structure here. */
    public MyQueue() {
        stackIn = new Stack<>(); // 负责进栈
        stackOut = new Stack<>(); // 负责出栈
    }
    
    /** Push element x to the back of queue. */
    public void push(int x) {
        stackIn.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    public int pop() {    
        dumpstackIn();
        return stackOut.pop();
    }
    
    /** Get the front element. */
    public int peek() {
        dumpstackIn();
        return stackOut.peek();
    }
    
    /** Returns whether the queue is empty. */
    public boolean empty() {
        return stackIn.isEmpty() && stackOut.isEmpty();
    }

    // 如果stackOut为空，那么将stackIn中的元素全部放到stackOut中
    private void dumpstackIn(){
        if (!stackOut.isEmpty()) return; 
        while (!stackIn.isEmpty()){
                stackOut.push(stackIn.pop());
        }
    }
}

Python：

class MyQueue:

    def __init__(self):
        """
        in主要负责push，out主要负责pop
        """
        self.stack_in = []
        self.stack_out = []


    def push(self, x: int) -> None:
        """
        有新元素进来，就往in里面push
        """
        self.stack_in.append(x)


    def pop(self) -> int:
        """
        Removes the element from in front of queue and returns that element.
        """
        if self.empty():
            return None
        
        if self.stack_out:
            return self.stack_out.pop()
        else:
            for i in range(len(self.stack_in)):
                self.stack_out.append(self.stack_in.pop())
            return self.stack_out.pop()


    def peek(self) -> int:
        """
        Get the front element.
        """
        ans = self.pop()
        self.stack_out.append(ans)
        return ans


    def empty(self) -> bool:
        """
        只要in或者out有元素，说明队列不为空
        """
        return not (self.stack_in or self.stack_out)

Go：

// 通过切片实现一个栈
// 由于只是辅助实现算法题目，因此不做异常情况处理
type MyStack []int

func (s *MyStack) Push(v int) {
	*s = append(*s, v)
}

func (s *MyStack) Pop() int {
	val := (*s)[len(*s)-1]
	*s = (*s)[:len(*s)-1]
	return val
}

func (s *MyStack) Peek() int {
	return (*s)[len(*s)-1]
}

func (s *MyStack) Size() int {
	return len(*s)
}

func (s *MyStack) Empty() bool {
	return s.Size() == 0
}

// ---------- 分界线 ----------

type MyQueue struct {
    stackIn *MyStack
    stackOut *MyStack
}


func Constructor() MyQueue {
    return MyQueue {
        stackIn: &MyStack{},
        stackOut: &MyStack{},
    }
}


func (this *MyQueue) Push(x int)  {
    this.stackIn.Push(x)
}


func (this *MyQueue) Pop() int {
    this.fillStackOut()
    return this.stackOut.Pop()
}


func (this *MyQueue) Peek() int {
    this.fillStackOut()
    return this.stackOut.Peek()
}


func (this *MyQueue) Empty() bool {
    return this.stackIn.Empty() && this.stackOut.Empty()
}

// fillStackOut 填充输出栈
func (this *MyQueue) fillStackOut() {
    if this.stackOut.Empty() {
        for !this.stackIn.Empty() {
            val := this.stackIn.Pop()
            this.stackOut.Push(val)        
        }
    }
}

JavaScript:

// 使用两个数组的栈方法（push, pop） 实现队列
/**
* Initialize your data structure here.
*/
var MyQueue = function() {
   this.stackIn = [];
   this.stackOut = [];
};

/**
* Push element x to the back of queue. 
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function(x) {
   this.stackIn.push(x);
};

/**
* Removes the element from in front of queue and returns that element.
* @return {number}
*/
MyQueue.prototype.pop = function() {
   const size = this.stackOut.length;
   if(size) {
       return this.stackOut.pop();
   }
   while(this.stackIn.length) {
       this.stackOut.push(this.stackIn.pop());
   }
   return this.stackOut.pop();
};

/**
* Get the front element.
* @return {number}
*/
MyQueue.prototype.peek = function() {
   const x = this.pop();
   this.stackOut.push(x);
   return x;
};

/**
* Returns whether the queue is empty.
* @return {boolean}
*/
MyQueue.prototype.empty = function() {
   return !this.stackIn.length && !this.stackOut.length
};

TypeScript:

class MyQueue {
    private stackIn: number[]
    private stackOut: number[]
    constructor() {
        this.stackIn = [];
        this.stackOut = [];
    }

    push(x: number): void {
        this.stackIn.push(x);
    }

    pop(): number {
        if (this.stackOut.length === 0) {
            while (this.stackIn.length > 0) {
                this.stackOut.push(this.stackIn.pop()!);
            }
        }
        return this.stackOut.pop()!;
    }

    peek(): number {
        let temp: number = this.pop();
        this.stackOut.push(temp);
        return temp;
    }

    empty(): boolean {
        return this.stackIn.length === 0 && this.stackOut.length === 0;
    }
}

Swift：

class MyQueue {
    
    var stackIn = [Int]()
    var stackOut = [Int]()
    
    init() {}
    
    /** Push element x to the back of queue. */
    func push(_ x: Int) {
        stackIn.append(x)
    }
    
    /** Removes the element from in front of queue and returns that element. */
    func pop() -> Int {
        if stackOut.isEmpty {
            while !stackIn.isEmpty {
                stackOut.append(stackIn.popLast()!)
            }
        }
        return stackOut.popLast() ?? -1
    }
    
    /** Get the front element. */
    func peek() -> Int {
        let res = pop()
        stackOut.append(res)
        return res
    }
    
    /** Returns whether the queue is empty. */
    func empty() -> Bool {
        return stackIn.isEmpty && stackOut.isEmpty
    }
}

C:

/*
1.两个type为int的数组（栈），大小为100
    第一个栈stackIn用来存放数据，第二个栈stackOut作为辅助用来输出数据
2.两个指针stackInTop和stackOutTop，分别指向栈顶
*/
typedef struct {
    int stackInTop, stackOutTop;
    int stackIn[100], stackOut[100];
} MyQueue;

/*
1.开辟一个队列的大小空间
2.将指针stackInTop和stackOutTop初始化为0
3.返回开辟的队列
*/
MyQueue* myQueueCreate() {
    MyQueue* queue = (MyQueue*)malloc(sizeof(MyQueue));
    queue->stackInTop = 0;
    queue->stackOutTop = 0;
    return queue;
}

/*
将元素存入第一个栈中,存入后栈顶指针+1
*/
void myQueuePush(MyQueue* obj, int x) {
    obj->stackIn[(obj->stackInTop)++] = x;
}

/*
1.若输出栈为空且当第一个栈中有元素（stackInTop>0时），将第一个栈中元素复制到第二个栈中（stackOut[stackTop2++] = stackIn[--stackTop1])
2.将栈顶元素保存
3.当stackTop2>0时，将第二个栈中元素复制到第一个栈中(stackIn[stackTop1++] = stackOut[--stackTop2])
*/
int myQueuePop(MyQueue* obj) {
    //优化：复制栈顶指针，减少对内存的访问次数
    int stackInTop = obj->stackInTop;
    int stackOutTop = obj->stackOutTop;
    //若输出栈为空
    if(stackOutTop == 0) {
        //将第一个栈中元素复制到第二个栈中
        while(stackInTop > 0) {
            obj->stackOut[stackOutTop++] = obj->stackIn[--stackInTop];
        }
    }
    //将第二个栈中栈顶元素（队列的第一个元素）出栈，并保存
    int top = obj->stackOut[--stackOutTop];
    //将输出栈中元素放回输入栈中
    while(stackOutTop > 0) {
        obj->stackIn[stackInTop++] = obj->stackOut[--stackOutTop];
    }
    //更新栈顶指针
    obj->stackInTop = stackInTop;
    obj->stackOutTop = stackOutTop;
    //返回队列中第一个元素
    return top;
}

//返回输入栈中的栈底元素
int myQueuePeek(MyQueue* obj) {
    return obj->stackIn[0];
}

//若栈顶指针均为0，则代表队列为空
bool myQueueEmpty(MyQueue* obj) {
    return obj->stackInTop == 0 && obj->stackOutTop == 0;
}

//将栈顶指针置0
void myQueueFree(MyQueue* obj) {
    obj->stackInTop = 0;
    obj->stackOutTop = 0;
}

C#:

public class MyQueue {
    Stack<int> inStack;
    Stack<int> outStack;

    public MyQueue() {
        inStack = new Stack<int>();// 负责进栈
        outStack = new Stack<int>();// 负责出栈
    }
    
    public void Push(int x) {
        inStack.Push(x);
    }
    
    public int Pop() {
        dumpstackIn();
        return outStack.Pop();
    }
    
    public int Peek() {
        dumpstackIn();
        return outStack.Peek();
    }
    
    public bool Empty() {
        return inStack.Count == 0 && outStack.Count == 0;
    }

    // 处理方法：
    // 如果outStack为空，那么将inStack中的元素全部放到outStack中
    private void dumpstackIn(){
        if (outStack.Count != 0) return; 
        while(inStack.Count != 0){
            outStack.Push(inStack.Pop());
        }
    }
}

PHP:

// SplStack 类通过使用一个双向链表来提供栈的主要功能。[PHP 5 >= 5.3.0, PHP 7, PHP 8]
// https://www.php.net/manual/zh/class.splstack.php
class MyQueue {
    // 双栈模拟队列：In栈存储数据；Out栈辅助处理
    private $stackIn;
    private $stackOut;
    
    function __construct() {
        $this->stackIn = new SplStack();
        $this->stackOut = new SplStack();
    }

    // In: 1 2 3  <= push  
    function push($x) {
        $this->stackIn->push($x);
    }

    function pop() {
        $this->peek();
        return $this->stackOut->pop();
    }

    function peek() {
        if($this->stackOut->isEmpty()){
            $this->shift();
        }
        return $this->stackOut->top();
    }

    function empty() {
        return $this->stackOut->isEmpty() && $this->stackIn->isEmpty();
    }

    // 如果Out栈为空，把In栈数据压入Out栈
    // In: 1 2 3 => pop    push => 1 2 3 :Out  
    private function shift(){
        while(!$this->stackIn->isEmpty()){
            $this->stackOut->push($this->stackIn->pop());
        }
    }
    }

Scala:

class MyQueue() {
  import scala.collection.mutable
  val stackIn = mutable.Stack[Int]() // 负责出栈
  val stackOut = mutable.Stack[Int]() // 负责入栈

  // 添加元素
  def push(x: Int) {
    stackIn.push(x)
  }

  // 复用代码，如果stackOut为空就把stackIn的所有元素都压入StackOut
  def dumpStackIn(): Unit = {
    if (!stackOut.isEmpty) return
    while (!stackIn.isEmpty) {
      stackOut.push(stackIn.pop())
    }
  }

  // 弹出元素
  def pop(): Int = {
    dumpStackIn()
    stackOut.pop()
  }

  // 获取队头
  def peek(): Int = {
    dumpStackIn()
    val res: Int = stackOut.pop()
    stackOut.push(res)
    res
  }

  // 判断是否为空
  def empty(): Boolean = {
    stackIn.isEmpty && stackOut.isEmpty
  }

}

Rust:

struct MyQueue {
    stack_in: Vec<i32>,
    stack_out: Vec<i32>,
}
impl MyQueue {
    fn new() -> Self {
        MyQueue {
            stack_in: Vec::new(),
            stack_out: Vec::new(),
        }
        
    }
    
    fn push(&mut self, x: i32) {
        self.stack_in.push(x);
    }
    
    fn pop(&mut self) -> i32 {
        if self.stack_out.is_empty(){
            while !self.stack_in.is_empty() {
                self.stack_out.push(self.stack_in.pop().unwrap());
            }
        }
        self.stack_out.pop().unwrap()
    }
    
    fn peek(&mut self) -> i32 {
        let res = self.pop();
        self.stack_out.push(res);
        res
    }
    
    fn empty(&self) -> bool {
       self.stack_in.is_empty() && self.stack_out.is_empty()
    }
}