- 做项目(多个C++、Java、Go、测开、前端项目) (opens new window)
- 刷算法(两个月高强度学算法) (opens new window)
- 背八股(40天挑战高频面试题) (opens new window)
这不仅仅是一道好题,也展现出计算机的思考方式
# 150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的运算符包括 + , - , * , / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
- 输入: ["2", "1", "+", "3", " * "]
- 输出: 9
- 解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
- 输入: ["4", "13", "5", "/", "+"]
- 输出: 6
- 解释: 该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入: ["10", "6", "9", "3", "+", "-11", " * ", "/", " * ", "17", "+", "5", "+"]
输出: 22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 221
2
3
4
5
6
7
逆波兰表达式:是一种后缀表达式,所谓后缀就是指运算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中。
# 算法公开课
《代码随想录》算法视频公开课 (opens new window):栈的最后表演! | LeetCode:150. 逆波兰表达式求值 (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
# 思路
# 正题
在上一篇文章中1047.删除字符串中的所有相邻重复项 (opens new window)提到了 递归就是用栈来实现的。
所以栈与递归之间在某种程度上是可以转换的! 这一点我们在后续讲解二叉树的时候,会更详细的讲解到。
那么来看一下本题,其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点,按照后序遍历的规则画出一个二叉树。
但我们没有必要从二叉树的角度去解决这个问题,只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了,就可以了。
在进一步看,本题中每一个子表达式要得出一个结果,然后拿这个结果再进行运算,那么这岂不就是一个相邻字符串消除的过程,和1047.删除字符串中的所有相邻重复项 (opens new window)中的对对碰游戏是不是就非常像了。
如动画所示:
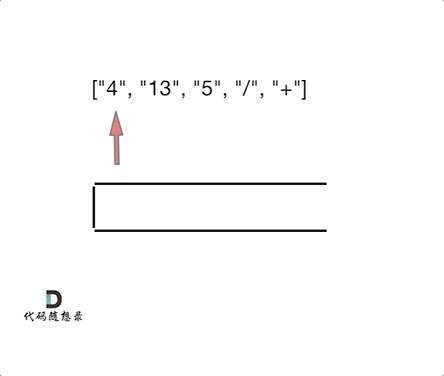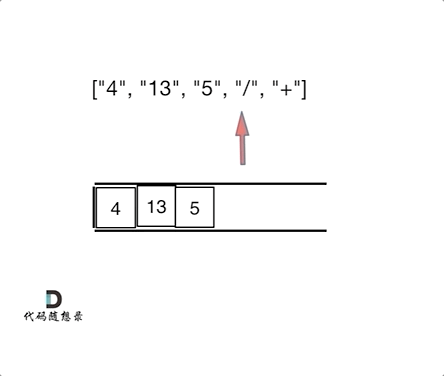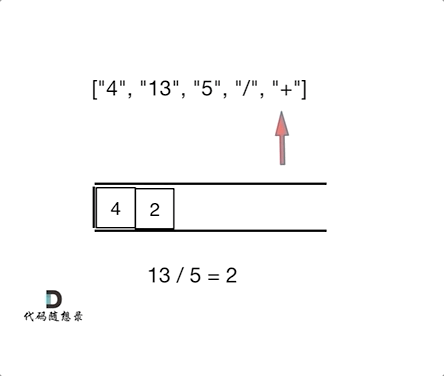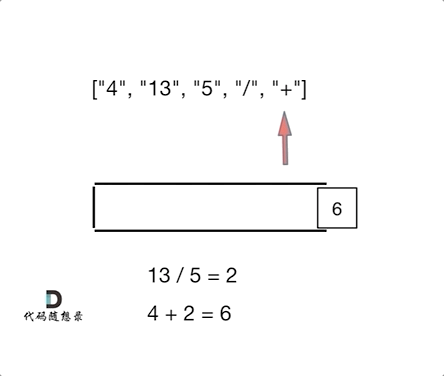
相信看完动画大家应该知道,这和1047. 删除字符串中的所有相邻重复项 (opens new window)是差不多的,只不过本题不要相邻元素做消除了,而是做运算!
C++代码如下:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
// 力扣修改了后台测试数据,需要用longlong
stack<long long> st;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
long long num1 = st.top();
st.pop();
long long num2 = st.top();
st.pop();
if (tokens[i] == "+") st.push(num2 + num1);
if (tokens[i] == "-") st.push(num2 - num1);
if (tokens[i] == "*") st.push(num2 * num1);
if (tokens[i] == "/") st.push(num2 / num1);
} else {
st.push(stoll(tokens[i]));
}
}
long long result = st.top();
st.pop(); // 把栈里最后一个元素弹出(其实不弹出也没事)
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
- 时间复杂度: O(n)
- 空间复杂度: O(n)
# 题外话
我们习惯看到的表达式都是中缀表达式,因为符合我们的习惯,但是中缀表达式对于计算机来说就不是很友好了。
例如:4 + 13 / 5,这就是中缀表达式,计算机从左到右去扫描的话,扫到13,还要判断13后面是什么运算符,还要比较一下优先级,然后13还和后面的5做运算,做完运算之后,还要向前回退到 4 的位置,继续做加法,你说麻不麻烦!
那么将中缀表达式,转化为后缀表达式之后:["4", "13", "5", "/", "+"] ,就不一样了,计算机可以利用栈来顺序处理,不需要考虑优先级了。也不用回退了, 所以后缀表达式对计算机来说是非常友好的。
可以说本题不仅仅是一道好题,也展现出计算机的思考方式。
在1970年代和1980年代,惠普在其所有台式和手持式计算器中都使用了RPN(后缀表达式),直到2020年代仍在某些模型中使用了RPN。
参考维基百科如下:
During the 1970s and 1980s, Hewlett-Packard used RPN in all of their desktop and hand-held calculators, and continued to use it in some models into the 2020s.
# 其他语言版本
# Java:
class Solution {
public int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList();
for (String s : tokens) {
if ("+".equals(s)) { // leetcode 内置jdk的问题,不能使用==判断字符串是否相等
stack.push(stack.pop() + stack.pop()); // 注意 - 和/ 需要特殊处理
} else if ("-".equals(s)) {
stack.push(-stack.pop() + stack.pop());
} else if ("*".equals(s)) {
stack.push(stack.pop() * stack.pop());
} else if ("/".equals(s)) {
int temp1 = stack.pop();
int temp2 = stack.pop();
stack.push(temp2 / temp1);
} else {
stack.push(Integer.valueOf(s));
}
}
return stack.pop();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Python3:
from operator import add, sub, mul
def div(x, y):
# 使用整数除法的向零取整方式
return int(x / y) if x * y > 0 else -(abs(x) // abs(y))
class Solution(object):
op_map = {'+': add, '-': sub, '*': mul, '/': div}
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for token in tokens:
if token not in {'+', '-', '*', '/'}:
stack.append(int(token))
else:
op2 = stack.pop()
op1 = stack.pop()
stack.append(self.op_map[token](op1, op2)) # 第一个出来的在运算符后面
return stack.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
另一种可行,但因为使用eval()相对较慢的方法:
class Solution(object):
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for token in tokens:
# 判断是否为数字,因为isdigit()不识别负数,故需要排除第一位的符号
if token.isdigit() or (len(token)>1 and token[1].isdigit()):
stack.append(token)
else:
op2 = stack.pop()
op1 = stack.pop()
# 由题意"The division always truncates toward zero",所以使用int()可以天然取整
stack.append(str(int(eval(op1 + token + op2))))
return int(stack.pop())
2
3
4
5
6
7
8
9
10
11
12
13
# Go:
func evalRPN(tokens []string) int {
stack := []int{}
for _, token := range tokens {
val, err := strconv.Atoi(token)
if err == nil {
stack = append(stack, val)
} else { // 如果err不为nil说明不是数字
num1, num2 := stack[len(stack)-2], stack[(len(stack))-1]
stack = stack[:len(stack)-2]
switch token {
case "+":
stack = append(stack, num1+num2)
case "-":
stack = append(stack, num1-num2)
case "*":
stack = append(stack, num1*num2)
case "/":
stack = append(stack, num1/num2)
}
}
}
return stack[0]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# JavaScript:
var evalRPN = function (tokens) {
const stack = [];
for (const token of tokens) {
if (isNaN(Number(token))) { // 非数字
const n2 = stack.pop(); // 出栈两个数字
const n1 = stack.pop();
switch (token) { // 判断运算符类型,算出新数入栈
case "+":
stack.push(n1 + n2);
break;
case "-":
stack.push(n1 - n2);
break;
case "*":
stack.push(n1 * n2);
break;
case "/":
stack.push(n1 / n2 | 0);
break;
}
} else { // 数字
stack.push(Number(token));
}
}
return stack[0]; // 因没有遇到运算符而待在栈中的结果
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# TypeScript:
普通版:
function evalRPN(tokens: string[]): number {
let helperStack: number[] = [];
let temp: number;
let i: number = 0;
while (i < tokens.length) {
let t: string = tokens[i];
switch (t) {
case '+':
temp = helperStack.pop()! + helperStack.pop()!;
helperStack.push(temp);
break;
case '-':
temp = helperStack.pop()!;
temp = helperStack.pop()! - temp;
helperStack.push(temp);
break;
case '*':
temp = helperStack.pop()! * helperStack.pop()!;
helperStack.push(temp);
break;
case '/':
temp = helperStack.pop()!;
temp = Math.trunc(helperStack.pop()! / temp);
helperStack.push(temp);
break;
default:
helperStack.push(Number(t));
break;
}
i++;
}
return helperStack.pop()!;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
优化版:
function evalRPN(tokens: string[]): number {
const helperStack: number[] = [];
const operatorMap: Map<string, (a: number, b: number) => number> = new Map([
['+', (a, b) => a + b],
['-', (a, b) => a - b],
['/', (a, b) => Math.trunc(a / b)],
['*', (a, b) => a * b],
]);
let a: number, b: number;
for (let t of tokens) {
if (operatorMap.has(t)) {
b = helperStack.pop()!;
a = helperStack.pop()!;
helperStack.push(operatorMap.get(t)!(a, b));
} else {
helperStack.push(Number(t));
}
}
return helperStack.pop()!;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Swift:
func evalRPN(_ tokens: [String]) -> Int {
var stack = [Int]()
for c in tokens {
let v = Int(c)
if let num = v {
// 遇到数字直接入栈
stack.append(num)
} else {
// 遇到运算符, 取出栈顶两元素计算, 结果压栈
var res: Int = 0
let num2 = stack.popLast()!
let num1 = stack.popLast()!
switch c {
case "+":
res = num1 + num2
case "-":
res = num1 - num2
case "*":
res = num1 * num2
case "/":
res = num1 / num2
default:
break
}
stack.append(res)
}
}
return stack.last!
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# C#:
public int EvalRPN(string[] tokens) {
int num;
Stack<int> stack = new Stack<int>();
foreach(string s in tokens){
if(int.TryParse(s, out num)){
stack.Push(num);
}else{
int num1 = stack.Pop();
int num2 = stack.Pop();
switch (s)
{
case "+":
stack.Push(num1 + num2);
break;
case "-":
stack.Push(num2 - num1);
break;
case "*":
stack.Push(num1 * num2);
break;
case "/":
stack.Push(num2 / num1);
break;
default:
break;
}
}
}
return stack.Pop();
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# PHP:
class Solution {
function evalRPN($tokens) {
$st = new SplStack();
for($i = 0;$i<count($tokens);$i++){
// 是数字直接入栈
if(is_numeric($tokens[$i])){
$st->push($tokens[$i]);
}else{
// 是符号进行运算
$num1 = $st->pop();
$num2 = $st->pop();
if ($tokens[$i] == "+") $st->push($num2 + $num1);
if ($tokens[$i] == "-") $st->push($num2 - $num1);
if ($tokens[$i] == "*") $st->push($num2 * $num1);
// 注意处理小数部分
if ($tokens[$i] == "/") $st->push(intval($num2 / $num1));
}
}
return $st->pop();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Scala:
object Solution {
import scala.collection.mutable
def evalRPN(tokens: Array[String]): Int = {
val stack = mutable.Stack[Int]() // 定义栈
// 抽取运算操作,需要传递x,y,和一个函数
def operator(x: Int, y: Int, f: (Int, Int) => Int): Int = f(x, y)
for (token <- tokens) {
// 模式匹配,匹配不同的操作符做什么样的运算
token match {
// 最后一个参数 _+_,代表x+y,遵循Scala的函数至简原则,以下运算同理
case "+" => stack.push(operator(stack.pop(), stack.pop(), _ + _))
case "-" => stack.push(operator(stack.pop(), stack.pop(), -_ + _))
case "*" => stack.push(operator(stack.pop(), stack.pop(), _ * _))
case "/" => {
var pop1 = stack.pop()
var pop2 = stack.pop()
stack.push(operator(pop2, pop1, _ / _))
}
case _ => stack.push(token.toInt) // 不是运算符就入栈
}
}
// 最后返回栈顶,不需要加return关键字
stack.pop()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Rust:
impl Solution {
pub fn eval_rpn(tokens: Vec<String>) -> i32 {
let mut stack = vec![];
for token in tokens.into_iter() {
match token.as_str() {
"+" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() += a;
}
"-" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() -= a;
}
"*" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() *= a;
}
"/" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() /= a;
}
_ => {
stack.push(token.parse::<i32>().unwrap());
}
}
}
stack.pop().unwrap()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# C:
int str_to_int(char *str) {
// string转integer
int num = 0, tens = 1;
for (int i = strlen(str) - 1; i >= 0; i--) {
if (str[i] == '-') {
num *= -1;
break;
}
num += (str[i] - '0') * tens;
tens *= 10;
}
return num;
}
int evalRPN(char** tokens, int tokensSize) {
int *stack = (int *)malloc(tokensSize * sizeof(int));
assert(stack);
int stackTop = 0;
for (int i = 0; i < tokensSize; i++) {
char symbol = (tokens[i])[0];
if (symbol < '0' && (tokens[i])[1] == '\0') {
// pop两个数字
int num1 = stack[--stackTop];
int num2 = stack[--stackTop];
// 计算结果
int result;
if (symbol == '+') {
result = num1 + num2;
} else if (symbol == '-') {
result = num2 - num1;
} else if (symbol == '/') {
result = num2 / num1;
} else {
result = num1 * num2;
}
// push回stack
stack[stackTop++] = result;
} else {
// push数字进stack
int num = str_to_int(tokens[i]);
stack[stackTop++] = num;
}
}
int result = stack[0];
free(stack);
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

评论
验证登录状态...