参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
统一写法是一种什么感觉
# 二叉树的统一迭代法
# 思路
此时我们在二叉树：一入递归深似海，从此offer是路人 (opens new window)中用递归的方式，实现了二叉树前中后序的遍历。
在二叉树：听说递归能做的，栈也能做！ (opens new window)中用栈实现了二叉树前后中序的迭代遍历（非递归）。
之后我们发现迭代法实现的先中后序，其实风格也不是那么统一，除了先序和后序，有关联，中序完全就是另一个风格了，一会用栈遍历，一会又用指针来遍历。
实践过的同学，也会发现使用迭代法实现先中后序遍历，很难写出统一的代码，不像是递归法，实现了其中的一种遍历方式，其他两种只要稍稍改一下节点顺序就可以了。
其实针对三种遍历方式，使用迭代法是可以写出统一风格的代码！
重头戏来了，接下来介绍一下统一写法。
我们以中序遍历为例，在二叉树：听说递归能做的，栈也能做！ (opens new window)中提到说使用栈的话，无法同时解决访问节点（遍历节点）和处理节点（将元素放进结果集）不一致的情况。
那我们就将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。
如何标记呢，就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
# 迭代法中序遍历
中序遍历代码如下：（详细注释）
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
if (node->right) st.push(node->right); // 添加右节点（空节点不入栈）
st.push(node); // 添加中节点
st.push(NULL); // 中节点访问过，但是还没有处理，加入空节点做为标记。
if (node->left) st.push(node->left); // 添加左节点（空节点不入栈）
} else { // 只有遇到空节点的时候，才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.top(); // 重新取出栈中元素
st.pop();
result.push_back(node->val); // 加入到结果集
}
}
return result;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
看代码有点抽象我们来看一下动画(中序遍历)：
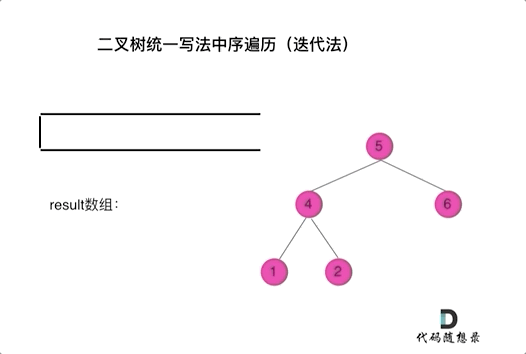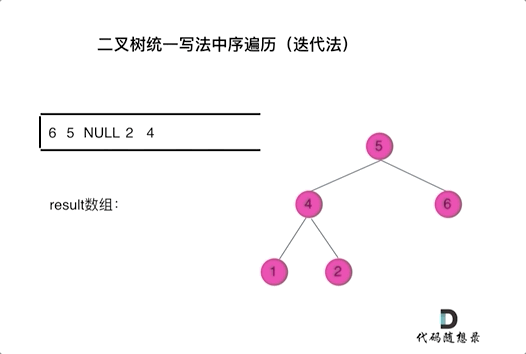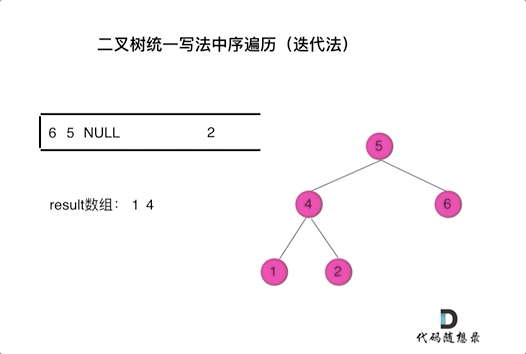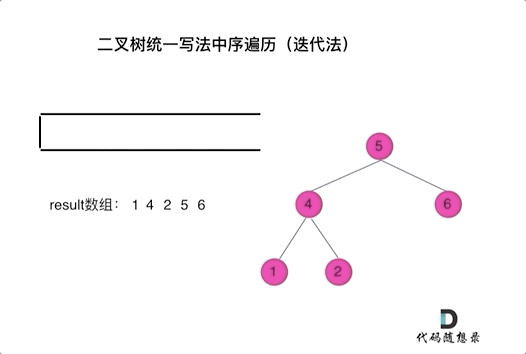
动画中，result数组就是最终结果集。
可以看出我们将访问的节点直接加入到栈中，但如果是处理的节点则后面放入一个空节点， 这样只有空节点弹出的时候，才将下一个节点放进结果集。
此时我们再来看前序遍历代码。
# 迭代法前序遍历
迭代法前序遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
st.push(node); // 中
st.push(NULL);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 迭代法后序遍历
后续遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 总结
此时我们写出了统一风格的迭代法，不用在纠结于前序写出来了，中序写不出来的情况了。
但是统一风格的迭代法并不好理解，而且想在面试直接写出来还有难度的。
所以大家根据自己的个人喜好，对于二叉树的前中后序遍历，选择一种自己容易理解的递归和迭代法。
# 其他语言版本
# Java：
迭代法前序遍历代码如下:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
if (node.right!=null) st.push(node.right); // 添加右节点（空节点不入栈）
if (node.left!=null) st.push(node.left); // 添加左节点（空节点不入栈）
st.push(node); // 添加中节点
st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
} else { // 只有遇到空节点的时候，才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
迭代法中序遍历代码如下:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
if (node.right!=null) st.push(node.right); // 添加右节点（空节点不入栈）
st.push(node); // 添加中节点
st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
if (node.left!=null) st.push(node.left); // 添加左节点（空节点不入栈）
} else { // 只有遇到空节点的时候，才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
迭代法后序遍历代码如下:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
st.push(node); // 添加中节点
st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
if (node.right!=null) st.push(node.right); // 添加右节点（空节点不入栈）
if (node.left!=null) st.push(node.left); // 添加左节点（空节点不入栈）
} else { // 只有遇到空节点的时候，才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Python：
迭代法前序遍历：
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
result = []
st= []
if root:
st.append(root)
while st:
node = st.pop()
if node != None:
if node.right: #右
st.append(node.right)
if node.left: #左
st.append(node.left)
st.append(node) #中
st.append(None)
else:
node = st.pop()
result.append(node.val)
return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
迭代法中序遍历：
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
result = []
st = []
if root:
st.append(root)
while st:
node = st.pop()
if node != None:
if node.right: #添加右节点（空节点不入栈）
st.append(node.right)
st.append(node) #添加中节点
st.append(None) #中节点访问过，但是还没有处理，加入空节点做为标记。
if node.left: #添加左节点（空节点不入栈）
st.append(node.left)
else: #只有遇到空节点的时候，才将下一个节点放进结果集
node = st.pop() #重新取出栈中元素
result.append(node.val) #加入到结果集
return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
迭代法后序遍历：
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
result = []
st = []
if root:
st.append(root)
while st:
node = st.pop()
if node != None:
st.append(node) #中
st.append(None)
if node.right: #右
st.append(node.right)
if node.left: #左
st.append(node.left)
else:
node = st.pop()
result.append(node.val)
return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Go：
前序遍历统一迭代法
/**
type Element struct {
// 元素保管的值
Value interface{}
// 内含隐藏或非导出字段
}
func (l *List) Back() *Element
前序遍历：中左右
压栈顺序：右左中
**/
func preorderTraversal(root *TreeNode) []int {
if root == nil {
return nil
}
var stack = list.New()//栈
res:=[]int{}//结果集
stack.PushBack(root)
var node *TreeNode
for stack.Len()>0{
e := stack.Back()
stack.Remove(e)//弹出元素
if e.Value==nil{// 如果为空，则表明是需要处理中间节点
e=stack.Back()//弹出元素（即中间节点）
stack.Remove(e)//删除中间节点
node=e.Value.(*TreeNode)
res=append(res,node.Val)//将中间节点加入到结果集中
continue//继续弹出栈中下一个节点
}
node = e.Value.(*TreeNode)
//压栈顺序：右左中
if node.Right!=nil{
stack.PushBack(node.Right)
}
if node.Left!=nil{
stack.PushBack(node.Left)
}
stack.PushBack(node)//中间节点压栈后再压入nil作为中间节点的标志符
stack.PushBack(nil)
}
return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
中序遍历统一迭代法
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
//中序遍历：左中右
//压栈顺序：右中左
func inorderTraversal(root *TreeNode) []int {
if root==nil{
return nil
}
stack:=list.New()//栈
res:=[]int{}//结果集
stack.PushBack(root)
var node *TreeNode
for stack.Len()>0{
e := stack.Back()
stack.Remove(e)
if e.Value==nil{// 如果为空，则表明是需要处理中间节点
e=stack.Back()//弹出元素（即中间节点）
stack.Remove(e)//删除中间节点
node=e.Value.(*TreeNode)
res=append(res,node.Val)//将中间节点加入到结果集中
continue//继续弹出栈中下一个节点
}
node = e.Value.(*TreeNode)
//压栈顺序：右中左
if node.Right!=nil{
stack.PushBack(node.Right)
}
stack.PushBack(node)//中间节点压栈后再压入nil作为中间节点的标志符
stack.PushBack(nil)
if node.Left!=nil{
stack.PushBack(node.Left)
}
}
return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
后序遍历统一迭代法
//后续遍历：左右中
//压栈顺序：中右左
func postorderTraversal(root *TreeNode) []int {
if root == nil {
return nil
}
var stack = list.New()//栈
res:=[]int{}//结果集
stack.PushBack(root)
var node *TreeNode
for stack.Len()>0{
e := stack.Back()
stack.Remove(e)
if e.Value==nil{// 如果为空，则表明是需要处理中间节点
e=stack.Back()//弹出元素（即中间节点）
stack.Remove(e)//删除中间节点
node=e.Value.(*TreeNode)
res=append(res,node.Val)//将中间节点加入到结果集中
continue//继续弹出栈中下一个节点
}
node = e.Value.(*TreeNode)
//压栈顺序：中右左
stack.PushBack(node)//中间节点压栈后再压入nil作为中间节点的标志符
stack.PushBack(nil)
if node.Right!=nil{
stack.PushBack(node.Right)
}
if node.Left!=nil{
stack.PushBack(node.Left)
}
}
return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# JavaScript:
前序遍历统一迭代法
// 前序遍历：中左右
// 压栈顺序：右左中
var preorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right); // 右
if (node.left) stack.push(node.left); // 左
stack.push(node); // 中
stack.push(null);
};
return res;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
中序遍历统一迭代法
// 中序遍历：左中右
// 压栈顺序：右中左
var inorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right); // 右
stack.push(node); // 中
stack.push(null);
if (node.left) stack.push(node.left); // 左
};
return res;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
后序遍历统一迭代法
// 后续遍历：左右中
// 压栈顺序：中右左
var postorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
stack.push(node); // 中
stack.push(null);
if (node.right) stack.push(node.right); // 右
if (node.left) stack.push(node.left); // 左
};
return res;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# TypeScript：
// 前序遍历（迭代法）
function preorderTraversal(root: TreeNode | null): number[] {
let helperStack: (TreeNode | null)[] = [];
let res: number[] = [];
let curNode: TreeNode | null;
if (root === null) return res;
helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop()!;
if (curNode !== null) {
if (curNode.right !== null) helperStack.push(curNode.right);
if (curNode.left !== null) helperStack.push(curNode.left);
helperStack.push(curNode);
helperStack.push(null);
} else {
curNode = helperStack.pop()!;
res.push(curNode.val);
}
}
return res;
};
// 中序遍历（迭代法）
function inorderTraversal(root: TreeNode | null): number[] {
let helperStack: (TreeNode | null)[] = [];
let res: number[] = [];
let curNode: TreeNode | null;
if (root === null) return res;
helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop()!;
if (curNode !== null) {
if (curNode.right !== null) helperStack.push(curNode.right);
helperStack.push(curNode);
helperStack.push(null);
if (curNode.left !== null) helperStack.push(curNode.left);
} else {
curNode = helperStack.pop()!;
res.push(curNode.val);
}
}
return res;
};
// 后序遍历（迭代法）
function postorderTraversal(root: TreeNode | null): number[] {
let helperStack: (TreeNode | null)[] = [];
let res: number[] = [];
let curNode: TreeNode | null;
if (root === null) return res;
helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop()!;
if (curNode !== null) {
helperStack.push(curNode);
helperStack.push(null);
if (curNode.right !== null) helperStack.push(curNode.right);
if (curNode.left !== null) helperStack.push(curNode.left);
} else {
curNode = helperStack.pop()!;
res.push(curNode.val);
}
}
return res;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# Scala:
// 前序遍历
object Solution {
import scala.collection.mutable
def preorderTraversal(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
val stack = mutable.Stack[TreeNode]()
if (root != null) stack.push(root)
while (!stack.isEmpty) {
var curNode = stack.top
if (curNode != null) {
stack.pop()
if (curNode.right != null) stack.push(curNode.right)
if (curNode.left != null) stack.push(curNode.left)
stack.push(curNode)
stack.push(null)
} else {
stack.pop()
res.append(stack.pop().value)
}
}
res.toList
}
}
// 中序遍历
object Solution {
import scala.collection.mutable
def inorderTraversal(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
val stack = mutable.Stack[TreeNode]()
if (root != null) stack.push(root)
while (!stack.isEmpty) {
var curNode = stack.top
if (curNode != null) {
stack.pop()
if (curNode.right != null) stack.push(curNode.right)
stack.push(curNode)
stack.push(null)
if (curNode.left != null) stack.push(curNode.left)
} else {
// 等于空的时候好办，弹出这个元素
stack.pop()
res.append(stack.pop().value)
}
}
res.toList
}
}
// 后序遍历
object Solution {
import scala.collection.mutable
def postorderTraversal(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
val stack = mutable.Stack[TreeNode]()
if (root != null) stack.push(root)
while (!stack.isEmpty) {
var curNode = stack.top
if (curNode != null) {
stack.pop()
stack.push(curNode)
stack.push(null)
if (curNode.right != null) stack.push(curNode.right)
if (curNode.left != null) stack.push(curNode.left)
} else {
stack.pop()
res.append(stack.pop().value)
}
}
res.toList
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
# Rust:
impl Solution{
// 前序
pub fn preorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut stack = vec![];
if root.is_some(){
stack.push(root);
}
while !stack.is_empty(){
if let Some(node) = stack.pop().unwrap(){
if node.borrow().right.is_some(){
stack.push(node.borrow().right.clone());
}
if node.borrow().left.is_some(){
stack.push(node.borrow().left.clone());
}
stack.push(Some(node));
stack.push(None);
}else{
res.push(stack.pop().unwrap().unwrap().borrow().val);
}
}
res
}
// 中序
pub fn inorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut stack = vec![];
if root.is_some() {
stack.push(root);
}
while !stack.is_empty() {
if let Some(node) = stack.pop().unwrap() {
if node.borrow().right.is_some() {
stack.push(node.borrow().right.clone());
}
stack.push(Some(node.clone()));
stack.push(None);
if node.borrow().left.is_some() {
stack.push(node.borrow().left.clone());
}
} else {
res.push(stack.pop().unwrap().unwrap().borrow().val);
}
}
res
}
// 后序
pub fn postorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut stack = vec![];
if root.is_some() {
stack.push(root);
}
while !stack.is_empty() {
if let Some(node) = stack.pop().unwrap() {
stack.push(Some(node.clone()));
stack.push(None);
if node.borrow().right.is_some() {
stack.push(node.borrow().right.clone());
}
if node.borrow().left.is_some() {
stack.push(node.borrow().left.clone());
}
} else {
res.push(stack.pop().unwrap().unwrap().borrow().val);
}
}
res
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
# C#
// 前序遍历
public IList<int> PreorderTraversal(TreeNode root)
{
var res = new List<int>();
var st = new Stack<TreeNode>();
if (root == null) return res;
st.Push(root);
while (st.Count != 0)
{
var node = st.Peek();
if (node == null)
{
st.Pop();
node = st.Peek();
st.Pop();
res.Add(node.val);
}
else
{
st.Pop();
if (node.right != null) st.Push(node.right);
if (node.left != null) st.Push(node.left);
st.Push(node);
st.Push(null);
}
}
return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 中序遍历
public IList<int> InorderTraversal(TreeNode root)
{
var res = new List<int>();
var st = new Stack<TreeNode>();
if (root == null) return res;
st.Push(root);
while (st.Count != 0)
{
var node = st.Peek();
if (node == null)
{
st.Pop();
node = st.Peek();
st.Pop();
res.Add(node.val);
}
else
{
st.Pop();
if (node.right != null) st.Push(node.right);
st.Push(node);
st.Push(null);
if (node.left != null) st.Push(node.left);
}
}
return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 后序遍历
public IList<int> PostorderTraversal(TreeNode root)
{
var res = new List<int>();
var st = new Stack<TreeNode>();
if (root == null) return res;
st.Push(root);
while (st.Count != 0)
{
var node = st.Peek();
if (node == null)
{
st.Pop();
node = st.Peek();
st.Pop();
res.Add(node.val);
}
else
{
st.Pop();
if (node.left != null) st.Push(node.left);
if (node.right != null) st.Push(node.right);
st.Push(node);
st.Push(null);
}
}
res.Reverse(0, res.Count);
return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
@2021-2024 代码随想录 版权所有 粤ICP备19156078号