# 704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
2
3
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
2
3
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
# 算法公开课
《代码随想录》算法视频公开课 (opens new window):手把手带你撕出正确的二分法 (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
# 思路
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当大家看到题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。
二分查找涉及的很多的边界条件,逻辑比较简单,但就是写不好。例如到底是 while(left < right) 还是 while(left <= right),到底是right = middle呢,还是要right = middle - 1呢?
大家写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
下面我用这两种区间的定义分别讲解两种不同的二分写法。
# 二分法第一种写法
第一种写法,我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
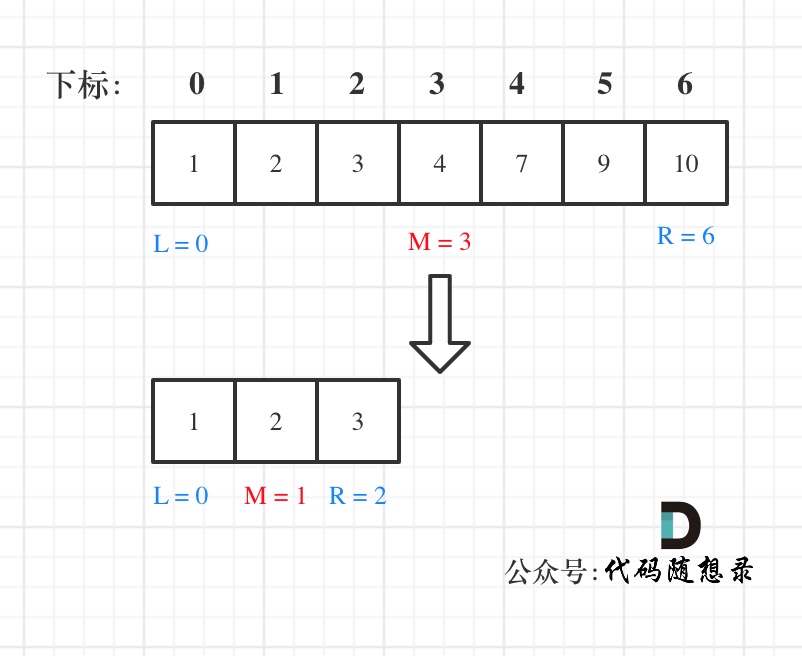
代码如下:(详细注释)
// 版本一
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
# 二分法第二种写法
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)
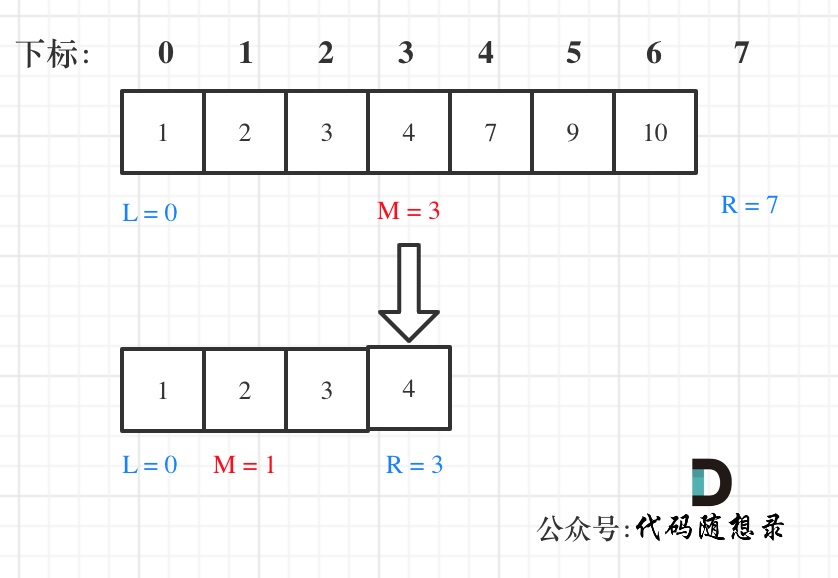
代码如下:(详细注释)
// 版本二
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
# 总结
二分法是非常重要的基础算法,为什么很多同学对于二分法都是一看就会,一写就废?
其实主要就是对区间的定义没有理解清楚,在循环中没有始终坚持根据查找区间的定义来做边界处理。
区间的定义就是不变量,那么在循环中坚持根据查找区间的定义来做边界处理,就是循环不变量规则。
本篇根据两种常见的区间定义,给出了两种二分法的写法,每一个边界为什么这么处理,都根据区间的定义做了详细介绍。
相信看完本篇应该对二分法有更深刻的理解了。
# 相关题目推荐
- 35.搜索插入位置 (opens new window)
- 34.在排序数组中查找元素的第一个和最后一个位置 (opens new window)
- 69.x 的平方根 (opens new window)
- 367.有效的完全平方数 (opens new window)
# 其他语言版本
# Java:
(版本一)左闭右闭区间
class Solution {
public int search(int[] nums, int target) {
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}
else if (nums[mid] < target) {
left = mid + 1;
}
else { // nums[mid] > target
right = mid - 1;
}
}
// 未找到目标值
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
(版本二)左闭右开区间
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}
else if (nums[mid] < target) {
left = mid + 1;
}
else { // nums[mid] > target
right = mid;
}
}
// 未找到目标值
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Python:
(版本一)左闭右闭区间
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1 # 定义target在左闭右闭的区间里,[left, right]
while left <= right:
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle - 1 # target在左区间,所以[left, middle - 1]
elif nums[middle] < target:
left = middle + 1 # target在右区间,所以[middle + 1, right]
else:
return middle # 数组中找到目标值,直接返回下标
return -1 # 未找到目标值
2
3
4
5
6
7
8
9
10
11
12
13
14
(版本二)左闭右开区间
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) # 定义target在左闭右开的区间里,即:[left, right)
while left < right: # 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle # target 在左区间,在[left, middle)中
elif nums[middle] < target:
left = middle + 1 # target 在右区间,在[middle + 1, right)中
else:
return middle # 数组中找到目标值,直接返回下标
return -1 # 未找到目标值
2
3
4
5
6
7
8
9
10
11
12
13
14
# Go:
(版本一)左闭右闭区间
// 时间复杂度 O(logn)
func search(nums []int, target int) int {
// 初始化左右边界
left := 0
right := len(nums) - 1
// 循环逐步缩小区间范围
for left <= right {
// 求区间中点
mid := left + (right-left)>>1
// 根据 nums[mid] 和 target 的大小关系
// 调整区间范围
if nums[mid] == target {
return mid
} else if nums[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
// 在输入数组内没有找到值等于 target 的元素
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
(版本二)左闭右开区间
// 时间复杂度 O(logn)
func search(nums []int, target int) int {
// 初始化左右边界
left := 0
right := len(nums)
// 循环逐步缩小区间范围
for left < right {
// 求区间中点
mid := left + (right-left)>>1
// 根据 nums[mid] 和 target 的大小关系
// 调整区间范围
if nums[mid] == target {
return mid
} else if nums[mid] < target {
left = mid + 1
} else {
right = mid
}
}
// 在输入数组内没有找到值等于 target 的元素
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# JavaScript:
(版本一)左闭右闭区间 [left, right]
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function(nums, target) {
// right是数组最后一个数的下标,num[right]在查找范围内,是左闭右闭区间
let mid, left = 0, right = nums.length - 1;
// 当left=right时,由于nums[right]在查找范围内,所以要包括此情况
while (left <= right) {
// 位运算 + 防止大数溢出
mid = left + ((right - left) >> 1);
// 如果中间数大于目标值,要把中间数排除查找范围,所以右边界更新为mid-1;如果右边界更新为mid,那中间数还在下次查找范围内
if (nums[mid] > target) {
right = mid - 1; // 去左面闭区间寻找
} else if (nums[mid] < target) {
left = mid + 1; // 去右面闭区间寻找
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
(版本二)左闭右开区间 [left, right)
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function(nums, target) {
// right是数组最后一个数的下标+1,nums[right]不在查找范围内,是左闭右开区间
let mid, left = 0, right = nums.length;
// 当left=right时,由于nums[right]不在查找范围,所以不必包括此情况
while (left < right) {
// 位运算 + 防止大数溢出
mid = left + ((right - left) >> 1);
// 如果中间值大于目标值,中间值不应在下次查找的范围内,但中间值的前一个值应在;
// 由于right本来就不在查找范围内,所以将右边界更新为中间值,如果更新右边界为mid-1则将中间值的前一个值也踢出了下次寻找范围
if (nums[mid] > target) {
right = mid; // 去左区间寻找
} else if (nums[mid] < target) {
left = mid + 1; // 去右区间寻找
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# TypeScript
(版本一)左闭右闭区间
function search(nums: number[], target: number): number {
let mid: number, left: number = 0, right: number = nums.length - 1;
while (left <= right) {
// 位运算 + 防止大数溢出
mid = left + ((right - left) >> 1);
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(版本二)左闭右开区间
function search(nums: number[], target: number): number {
let mid: number, left: number = 0, right: number = nums.length;
while (left < right) {
// 位运算 + 防止大数溢出
mid = left +((right - left) >> 1);
if (nums[mid] > target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Ruby:
# (版本一)左闭右闭区间
def search(nums, target)
left, right = 0, nums.length - 1
while left <= right # 由于定义target在一个在左闭右闭的区间里,因此极限情况下存在left==right
middle = (left + right) / 2
if nums[middle] > target
right = middle - 1
elsif nums[middle] < target
left = middle + 1
else
return middle # return兼具返回与跳出循环的作用
end
end
-1
end
# (版本二)左闭右开区间
def search(nums, target)
left, right = 0, nums.length
while left < right # 由于定义target在一个在左闭右开的区间里,因此极限情况下right=left+1
middle = (left + right) / 2
if nums[middle] > target
right = middle
elsif nums[middle] < target
left = middle + 1
else
return middle
end
end
-1
end
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Swift:
// (版本一)左闭右闭区间
func search(nums: [Int], target: Int) -> Int {
// 1. 先定义区间。这里的区间是[left, right]
var left = 0
var right = nums.count - 1
while left <= right {// 因为taeget是在[left, right]中,包括两个边界值,所以这里的left == right是有意义的
// 2. 计算区间中间的下标(如果left、right都比较大的情况下,left + right就有可能会溢出)
// let middle = (left + right) / 2
// 防溢出:
let middle = left + (right - left) / 2
// 3. 判断
if target < nums[middle] {
// 当目标在区间左侧,就需要更新右边的边界值,新区间为[left, middle - 1]
right = middle - 1
} else if target > nums[middle] {
// 当目标在区间右侧,就需要更新左边的边界值,新区间为[middle + 1, right]
left = middle + 1
} else {
// 当目标就是在中间,则返回中间值的下标
return middle
}
}
// 如果找不到目标,则返回-1
return -1
}
// (版本二)左闭右开区间
func search(nums: [Int], target: Int) -> Int {
var left = 0
var right = nums.count
while left < right {
let middle = left + ((right - left) >> 1)
if target < nums[middle] {
right = middle
} else if target > nums[middle] {
left = middle + 1
} else {
return middle
}
}
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# Rust:
(版本一)左闭右闭区间
use std::cmp::Ordering;
impl Solution {
pub fn search(nums: Vec<i32>, target: i32) -> i32 {
let (mut left, mut right) = (0_i32, nums.len() as i32 - 1);
while left <= right {
let mid = (right + left) / 2;
match nums[mid as usize].cmp(&target) {
Ordering::Less => left = mid + 1,
Ordering::Greater => right = mid - 1,
Ordering::Equal => return mid,
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//(版本二)左闭右开区间
use std::cmp::Ordering;
impl Solution {
pub fn search(nums: Vec<i32>, target: i32) -> i32 {
let (mut left, mut right) = (0_i32, nums.len() as i32);
while left < right {
let mid = (right + left) / 2;
match nums[mid as usize].cmp(&target) {
Ordering::Less => left = mid + 1,
Ordering::Greater => right = mid,
Ordering::Equal => return mid,
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# C:
// (版本一) 左闭右闭区间 [left, right]
int search(int* nums, int numsSize, int target){
int left = 0;
int right = numsSize-1;
int middle = 0;
//若left小于等于right,说明区间中元素不为0
while(left<=right) {
//更新查找下标middle的值
middle = (left+right)/2;
//此时target可能会在[left,middle-1]区间中
if(nums[middle] > target) {
right = middle-1;
}
//此时target可能会在[middle+1,right]区间中
else if(nums[middle] < target) {
left = middle+1;
}
//当前下标元素等于target值时,返回middle
else if(nums[middle] == target){
return middle;
}
}
//若未找到target元素,返回-1
return -1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// (版本二) 左闭右开区间 [left, right)
int search(int* nums, int numsSize, int target){
int length = numsSize;
int left = 0;
int right = length; //定义target在左闭右开的区间里,即:[left, right)
int middle = 0;
while(left < right){ // left == right时,区间[left, right)属于空集,所以用 < 避免该情况
int middle = left + (right - left) / 2;
if(nums[middle] < target){
//target位于(middle , right) 中为保证集合区间的左闭右开性,可等价为[middle + 1,right)
left = middle + 1;
}else if(nums[middle] > target){
//target位于[left, middle)中
right = middle ;
}else{ // nums[middle] == target ,找到目标值target
return middle;
}
}
//未找到目标值,返回-1
return -1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# PHP:
// 左闭右闭区间
class Solution {
/**
* @param Integer[] $nums
* @param Integer $target
* @return Integer
*/
function search($nums, $target) {
if (count($nums) == 0) {
return -1;
}
$left = 0;
$right = count($nums) - 1;
while ($left <= $right) {
$mid = floor(($left + $right) / 2);
if ($nums[$mid] == $target) {
return $mid;
}
if ($nums[$mid] > $target) {
$right = $mid - 1;
}
else {
$left = $mid + 1;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# C#:
//左闭右闭
public class Solution {
public int Search(int[] nums, int target) {
int left = 0;
int right = nums.Length - 1;
while(left <= right){
int mid = (right - left ) / 2 + left;
if(nums[mid] == target){
return mid;
}
else if(nums[mid] < target){
left = mid+1;
}
else if(nums[mid] > target){
right = mid-1;
}
}
return -1;
}
}
//左闭右开
public class Solution{
public int Search(int[] nums, int target){
int left = 0;
int right = nums.Length;
while(left < right){
int mid = (right - left) / 2 + left;
if(nums[mid] == target){
return mid;
}
else if(nums[mid] < target){
left = mid + 1;
}
else if(nums[mid] > target){
right = mid;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# Kotlin:
class Solution {
fun search(nums: IntArray, target: Int): Int {
// leftBorder
var left:Int = 0
// rightBorder
var right:Int = nums.size - 1
// 使用左闭右闭区间
while (left <= right) {
var middle:Int = left + (right - left)/2
// taget 在左边
if (nums[middle] > target) {
right = middle - 1
}
else {
// target 在右边
if (nums[middle] < target) {
left = middle + 1
}
// 找到了,返回
else return middle
}
}
// 没找到,返回
return -1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Kotlin:
// (版本一)左闭右开区间
class Solution {
fun search(nums: IntArray, target: Int): Int {
var left = 0
var right = nums.size // [left,right) 右侧为开区间,right 设置为 nums.size
while (left < right) {
val mid = (left + right) / 2
if (nums[mid] < target) left = mid + 1
else if (nums[mid] > target) right = mid // 代码的核心,循环中 right 是开区间,这里也应是开区间
else return mid
}
return -1 // 没有找到 target ,返回 -1
}
}
// (版本二)左闭右闭区间
class Solution {
fun search(nums: IntArray, target: Int): Int {
var left = 0
var right = nums.size - 1 // [left,right] 右侧为闭区间,right 设置为 nums.size - 1
while (left <= right) {
val mid = (left + right) / 2
if (nums[mid] < target) left = mid + 1
else if (nums[mid] > target) right = mid - 1 // 代码的核心,循环中 right 是闭区间,这里也应是闭区间
else return mid
}
return -1 // 没有找到 target ,返回 -1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Scala:
(版本一)左闭右闭区间
object Solution {
def search(nums: Array[Int], target: Int): Int = {
var left = 0
var right = nums.length - 1
while (left <= right) {
var mid = left + ((right - left) / 2)
if (target == nums(mid)) {
return mid
} else if (target < nums(mid)) {
right = mid - 1
} else {
left = mid + 1
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(版本二)左闭右开区间
object Solution {
def search(nums: Array[Int], target: Int): Int = {
var left = 0
var right = nums.length
while (left < right) {
val mid = left + (right - left) / 2
if (target == nums(mid)) {
return mid
} else if (target < nums(mid)) {
right = mid
} else {
left = mid + 1
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Dart:
(版本一)左闭右闭区间
class Solution {
int search(List<int> nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int middle = ((left + right)/2).truncate();
switch (nums[middle].compareTo(target)) {
case 1:
right = middle - 1;
continue;
case -1:
left = middle + 1;
continue;
default:
return middle;
}
}
return -1;
}
}
(版本二)左闭右开区间
class Solution {
int search(List<int> nums, int target) {
int left = 0;
int right = nums.length;
while (left < right) {
int middle = left + ((right - left) >> 1);
switch (nums[middle].compareTo(target)) {
case 1:
right = middle;
continue;
case -1:
left = middle + 1;
continue;
default:
return middle;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43