代码随想录

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

# 27. 移除元素

力扣题目链接 (opens new window)

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。

示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

你不需要考虑数组中超出新长度后面的元素。

# 算法公开课

《代码随想录》算法视频公开课 (opens new window)：数组中移除元素并不容易！LeetCode：27. 移除元素 (opens new window)，相信结合视频再看本篇题解，更有助于大家对本题的理解。

# 思路

有的同学可能说了，多余的元素，删掉不就得了。

要知道数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

数组的基础知识可以看这里程序员算法面试中，必须掌握的数组理论知识 (opens new window)。

# 暴力解法

这个题目暴力的解法就是两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。

删除过程如下：

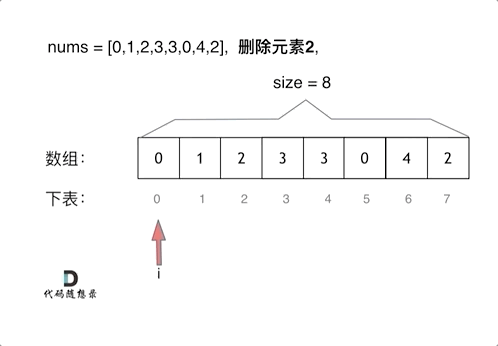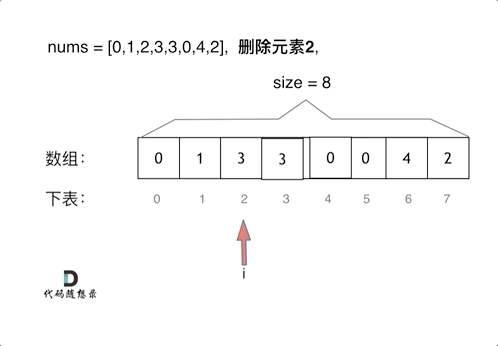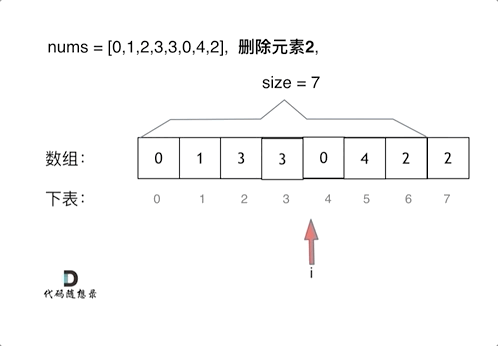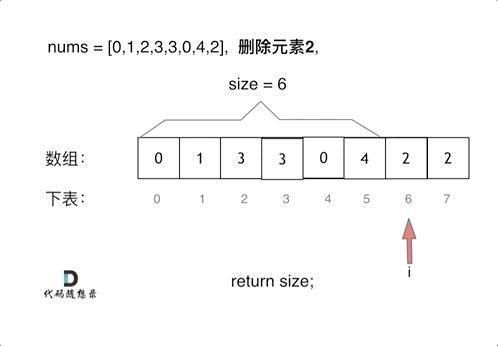
27.移除元素-暴力解法

很明显暴力解法的时间复杂度是O(n^2)，这道题目暴力解法在leetcode上是可以过的。

代码如下：

// 时间复杂度：O(n^2)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int size = nums.size();
        for (int i = 0; i < size; i++) {
            if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
                for (int j = i + 1; j < size; j++) {
                    nums[j - 1] = nums[j];
                }
                i--; // 因为下标i以后的数值都向前移动了一位，所以i也向前移动一位
                size--; // 此时数组的大小-1
            }
        }
        return size;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  • 时间复杂度：O(n^2)
  • 空间复杂度：O(1)

# 双指针法

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针

  • 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
  • 慢指针：指向更新 新数组下标的位置

很多同学这道题目做的很懵，就是不理解 快慢指针究竟都是什么含义，所以一定要明确含义，后面的思路就更容易理解了。

删除过程如下：

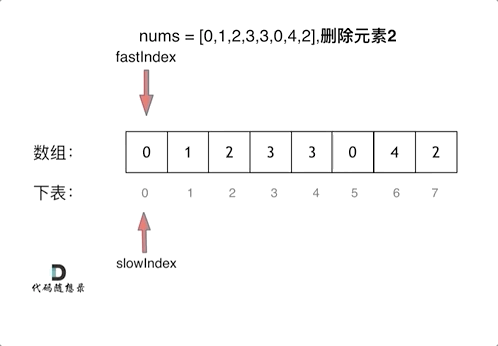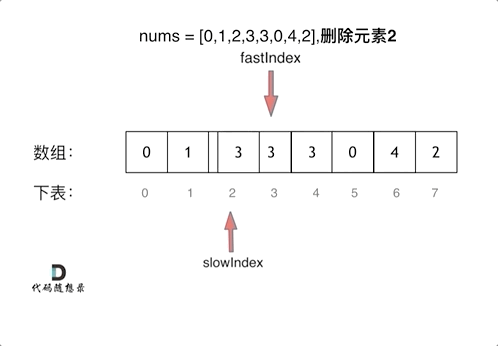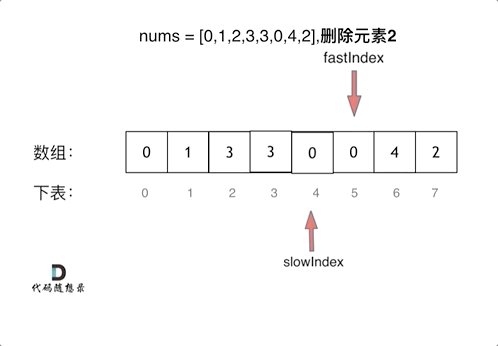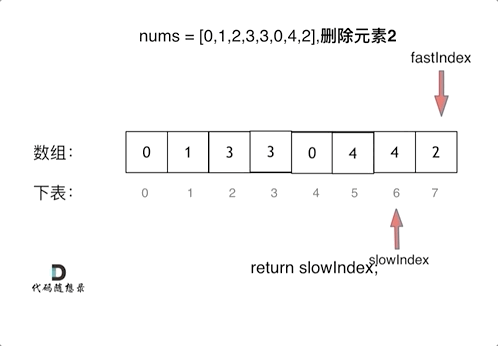
27.移除元素-双指针法

很多同学不了解

双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组、链表、字符串等操作的面试题，都使用双指针法。

后续都会一一介绍到，本题代码如下：

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
            if (val != nums[fastIndex]) {
                nums[slowIndex++] = nums[fastIndex];
            }
        }
        return slowIndex;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

注意这些实现方法并没有改变元素的相对位置！

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

# 相关题目推荐

# 其他语言版本

# Java：

class Solution {
    public int removeElement(int[] nums, int val) {
        // 快慢指针
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
            if (nums[fastIndex] != val) {
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
            }
        }
        return slowIndex;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
//相向双指针法
class Solution {
    public int removeElement(int[] nums, int val) {
        int left = 0;
        int right = nums.length - 1;
        while(right >= 0 && nums[right] == val) right--; //将right移到从右数第一个值不为val的位置
        while(left <= right) {
            if(nums[left] == val) { //left位置的元素需要移除
                //将right位置的元素移到left（覆盖），right位置移除
                nums[left] = nums[right];
                right--;
            }
            left++;
            while(right >= 0 && nums[right] == val) right--;
        }
        return left;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 相向双指针法（版本二）
class Solution {
    public int removeElement(int[] nums, int val) {
        int left = 0;
        int right = nums.length - 1;
        while(left <= right){
            if(nums[left] == val){
                nums[left] = nums[right];
                right--;
            }else {
                // 这里兼容了right指针指向的值与val相等的情况
                left++;
            }
        }
        return left;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# Python：

（版本一）快慢指针法
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        # 快慢指针
        fast = 0  # 快指针
        slow = 0  # 慢指针
        size = len(nums)
        while fast < size:  # 不加等于是因为，a = size 时，nums[a] 会越界
            # slow 用来收集不等于 val 的值，如果 fast 对应值不等于 val，则把它与 slow 替换
            if nums[fast] != val:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
        return slow
1
2
3
4
5
6
7
8
9
10
11
12
13
14
（版本二）暴力法
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        i, l = 0, len(nums)
        while i < l:
            if nums[i] == val: # 找到等于目标值的节点
                for j in range(i+1, l): # 移除该元素，并将后面元素向前平移
                    nums[j - 1] = nums[j]
                l -= 1
                i -= 1
            i += 1
        return l
1
2
3
4
5
6
7
8
9
10
11
12
13
# 相向双指针法
# 时间复杂度 O(n)
# 空间复杂度 O(1)
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        n = len(nums)
        left, right  = 0, n - 1
        while left <= right:
            while left <= right and nums[left] != val:
                left += 1
            while left <= right and nums[right] == val:
                right -= 1
            if left < right:
                nums[left] = nums[right]
                left += 1
                right -= 1
        return left
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# Go：

// 暴力法
// 时间复杂度 O(n^2)
// 空间复杂度 O(1)
func removeElement(nums []int, val int) int {
    size := len(nums)
    for i := 0; i < size; i ++ {
        if nums[i] == val {
            for j := i + 1; j < size; j ++ {
                nums[j - 1] = nums[j]
            }
            i --
            size --
        }
    }
    return size
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 快慢指针法
// 时间复杂度 O(n)
// 空间复杂度 O(1)
func removeElement(nums []int, val int) int {
	// 初始化慢指针 slow
	slow := 0
	// 通过 for 循环移动快指针 fast
	// 当 fast 指向的元素等于 val 时，跳过
	// 否则，将该元素写入 slow 指向的位置，并将 slow 后移一位
	for fast := 0; fast < len(nums); fast++ {
		if nums[fast] == val {
			continue
		}
		nums[slow] = nums[fast]
		slow++
	}

	return slow
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//相向双指针法
func removeElement(nums []int, val int) int {
    // 有点像二分查找的左闭右闭区间 所以下面是<=
	left := 0
	right := len(nums) - 1
	for left <= right {
		// 不断寻找左侧的val和右侧的非val 找到时交换位置 目的是将val全覆盖掉
		for left <= right && nums[left] != val {
			left++
		}
		for left <= right && nums[right] == val {
			right--
		}
		//各自找到后开始覆盖 覆盖后继续寻找
		if left < right {
			nums[left] = nums[right]
			left++
			right--
		}
	}
	return left
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# JavaScript:

//时间复杂度：O(n)
//空间复杂度：O(1)
var removeElement = (nums, val) => {
    let k = 0;
    for(let i = 0;i < nums.length;i++){
        if(nums[i] != val){
            nums[k++] = nums[i]
        }
    }
    return k;
};
1
2
3
4
5
6
7
8
9
10
11

# TypeScript：

function removeElement(nums: number[], val: number): number {
    let slowIndex: number = 0, fastIndex: number = 0;
    while (fastIndex < nums.length) {
        if (nums[fastIndex] !== val) {
            nums[slowIndex++] = nums[fastIndex];
        }
        fastIndex++;
    }
    return slowIndex;
};
1
2
3
4
5
6
7
8
9
10

# Ruby:

def remove_element(nums, val)
    i = 0
    nums.each_index do |j|
        if nums[j] != val
            nums[i] = nums[j]
            i+=1
        end
    end
    i
end
1
2
3
4
5
6
7
8
9
10

# Rust:

impl Solution {
    pub fn remove_element(nums: &mut Vec<i32>, val: i32) -> i32 {
        let mut slowIdx = 0;
        for pos in (0..nums.len()) {
            if nums[pos]!=val {
                nums[slowIdx] = nums[pos];
                slowIdx += 1;
            }
        }
        return (slowIdx) as i32;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

# Swift:

func removeElement(_ nums: inout [Int], _ val: Int) -> Int {
    var slowIndex = 0

    for fastIndex in 0..<nums.count {
        if val != nums[fastIndex] {
                nums[slowIndex] = nums[fastIndex]
                slowIndex += 1
        }
    }
    return slowIndex
}
1
2
3
4
5
6
7
8
9
10
11

# PHP:

class Solution {
    /**
     * @param Integer[] $nums
     * @param Integer $val
     * @return Integer
     */
    function removeElement(&$nums, $val) {
        if (count($nums) == 0) {
            return 0;
        }
        // 快慢指针
        $slow = 0;
        for ($fast = 0; $fast < count($nums); $fast++) {
            if ($nums[$fast] != $val) {
                $nums[$slow] = $nums[$fast];
                $slow++;
            }
        }
        return $slow;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# C:

int removeElement(int* nums, int numsSize, int val){
    int slow = 0;
    for(int fast = 0; fast < numsSize; fast++) {
        //若快指针位置的元素不等于要删除的元素
        if(nums[fast] != val) {
            //将其挪到慢指针指向的位置，慢指针+1
            nums[slow++] = nums[fast];
        }
    }
    //最后慢指针的大小就是新的数组的大小
    return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12

# Kotlin:

fun removeElement(nums: IntArray, `val`: Int): Int {
        var slowIndex = 0 // 初始化慢指针
        for (fastIndex in nums.indices) {
            if (nums[fastIndex] != `val`) nums[slowIndex++] = nums[fastIndex] // 在慢指针所在位置存储未被删除的元素
        }
        return slowIndex
    }
1
2
3
4
5
6
7

# Scala:

object Solution {
  def removeElement(nums: Array[Int], `val`: Int): Int = {
    var slow = 0
    for (fast <- 0 until nums.length) {
      if (`val` != nums(fast)) {
        nums(slow) = nums(fast)
        slow += 1
      }
    }
    slow
  }
}
1
2
3
4
5
6
7
8
9
10
11
12

# C#:

public class Solution {
    public int RemoveElement(int[] nums, int val) {
        int slow = 0;
        for (int fast = 0; fast < nums.Length; fast++) {
            if (val != nums[fast]) {
                nums[slow++] = nums[fast];
            }
        }
        return slow;
    }
}
1
2
3
4
5
6
7
8
9
10
11

###Dart:

int removeElement(List<int> nums, int val) {
    //相向双指针法
    var left = 0;
    var right = nums.length - 1;
    while (left <= right) {
	//寻找左侧的val，将其被右侧非val覆盖
        if (nums[left] == val) {
            while (nums[right] == val&&left<=right) {
                right--;
            if (right < 0) {
                return 0;
        }
      }
      nums[left] = nums[right--];
    } else {
      left++;
    }
  }
  //覆盖后可以将0至left部分视为所需部分
  return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
上次更新：: 8/22/2024, 9:07:28 PM

← 4. 有序数组的平方 →

@2021-2024 代码随想录 版权所有 粤ICP备19156078号