本周小结！（贪心算法系列四）

周一

在贪心算法：用最少数量的箭引爆气球 (opens new window)中，我们开始讲解了重叠区间问题，用最少的弓箭射爆所有气球，其本质就是找到最大的重叠区间。

按照左边界进行排序后，如果气球重叠了，重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭

如图：

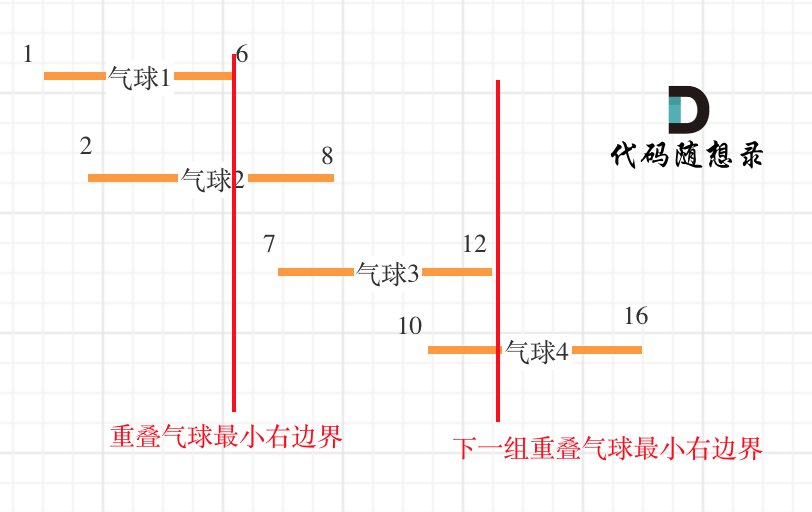
模拟射气球的过程，很多同学真的要去模拟了，实时把气球从数组中移走，这么写的话就复杂了，从前向后遍历重复的只要跳过就可以的。

周二

在贪心算法：无重叠区间 (opens new window)中要去掉最少的区间，来让所有区间没有重叠。

我来按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。

如图：

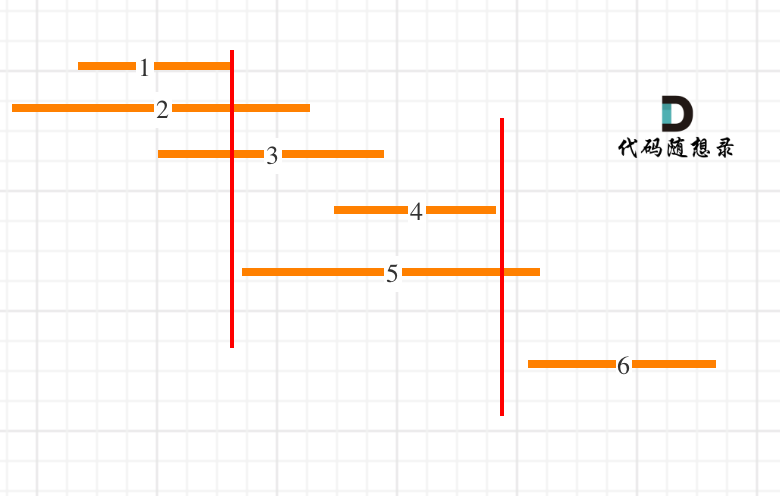
细心的同学就发现了，此题和 贪心算法：用最少数量的箭引爆气球 (opens new window)非常像。

弓箭的数量就相当于是非交叉区间的数量，只要把弓箭那道题目代码里射爆气球的判断条件加个等号（认为[0，1][1，2]不是相邻区间），然后用总区间数减去弓箭数量 就是要移除的区间数量了。

把贪心算法：用最少数量的箭引爆气球 (opens new window)代码稍做修改，就可以AC本题。

修改后的C++代码如下：

class Solution {
public:
    // 按照区间左边界从大到小排序
    static bool cmp (const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) return 0;
        sort(intervals.begin(), intervals.end(), cmp);

        int result = 1;
        for (int i = 1; i < intervals.size(); i++) {
            if (intervals[i][0] >= intervals[i - 1][1]) { // 需要要把> 改成 >= 就可以了
                result++; // 需要一支箭
            }
            else {
                intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // 更新重叠气球最小右边界
            }
        }
        return intervals.size() - result;
    }
};

周三

贪心算法：划分字母区间 (opens new window)中我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

这道题目leetcode上标的是贪心，其实我不认为是贪心，因为没感受到局部最优和全局最优的关系。

但不影响这是一道好题，思路很不错，通过字符出现最远距离取并集的方法，把出现过的字符都圈到一个区间里。

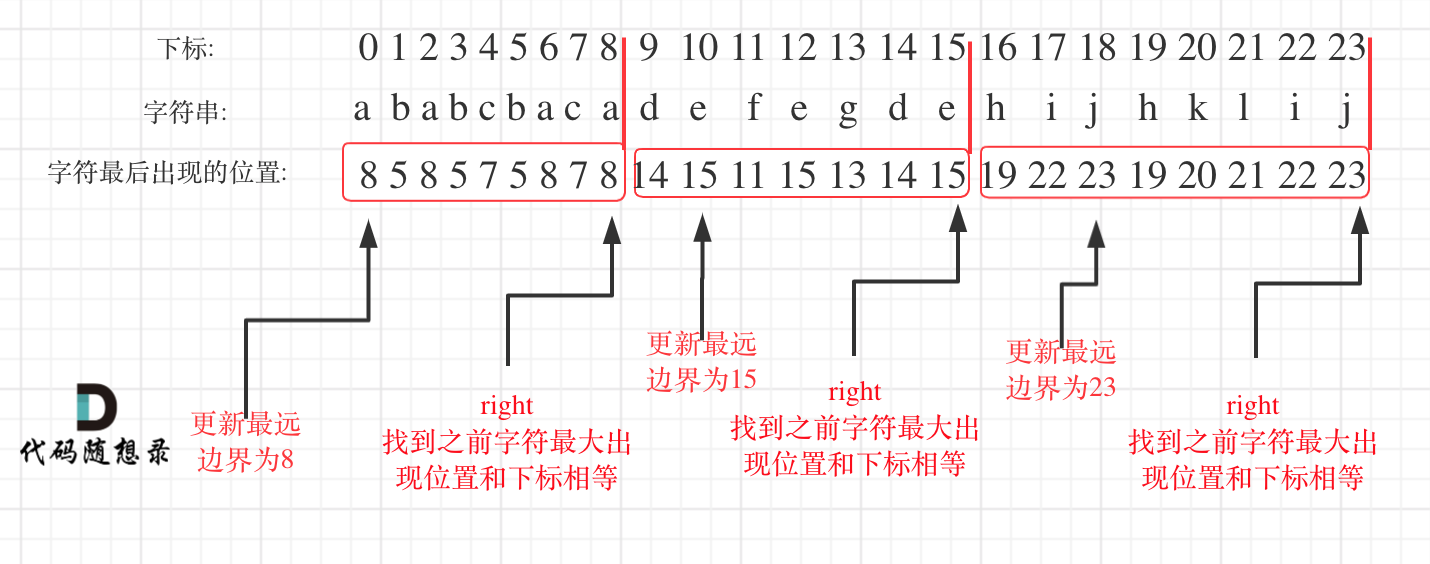
解题过程分如下两步：

• 统计每一个字符最后出现的位置
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

如图：

周四

贪心算法：合并区间 (opens new window)中要合并所有重叠的区间。

相信如果录友们前几天区间问题的题目认真练习了，今天题目就应该算简单一些了。

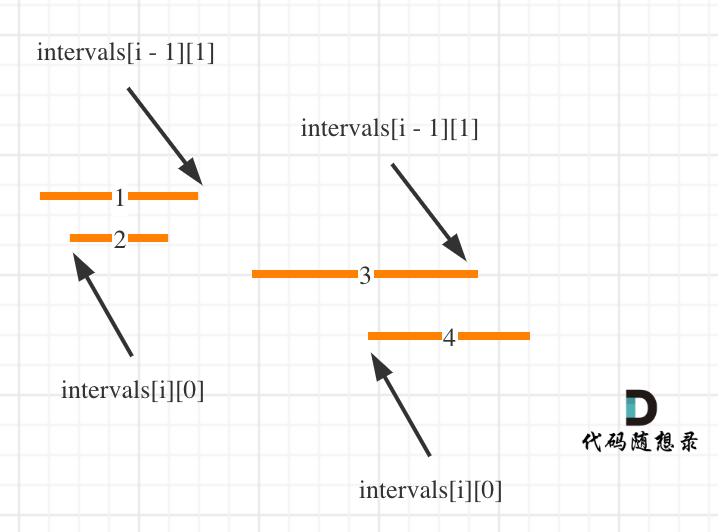
按照左边界排序，排序之后局部最优：每次合并都取最大的右边界，这样就可以合并更多的区间了，整体最优：合并所有重叠的区间。

具体操作：按照左边界从小到大排序之后，如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界，则一定有重复，因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。

如图：

总结

本周的主题就是用贪心算法来解决区间问题，经过本周的学习，大家应该对区间的各种合并分割有一定程度的了解了。

其实很多区间的合并操作看起来都是常识，其实贪心算法有时候就是常识，但也别小看了贪心算法。

在贪心算法：合并区间 (opens new window)中就说过，对于贪心算法，很多同学都是：「如果能凭常识直接做出来，就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了」。

所以还是要多看多做多练习！

「代码随想录」里总结的都是经典题目，大家跟着练就节省了不少选择题目的时间了。