- 做项目(多个C++、Java、Go、测开、前端项目) (opens new window)
- 刷算法(两个月高强度学算法) (opens new window)
- 背八股(40天挑战高频面试题) (opens new window)
# 435. 无重叠区间
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
- 输入: [ [1,2], [2,3], [3,4], [1,3] ]
- 输出: 1
- 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
- 输入: [ [1,2], [1,2], [1,2] ]
- 输出: 2
- 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
- 输入: [ [1,2], [2,3] ]
- 输出: 0
- 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
# 算法公开课
《代码随想录》算法视频公开课 (opens new window):贪心算法,依然是判断重叠区间 | LeetCode:435.无重叠区间 (opens new window),相信结合视频在看本篇题解,更有助于大家对本题的理解。
# 思路
相信很多同学看到这道题目都冥冥之中感觉要排序,但是究竟是按照右边界排序,还是按照左边界排序呢?
其实都可以。主要就是为了让区间尽可能的重叠。
我来按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
此时问题就是要求非交叉区间的最大个数。
这里记录非交叉区间的个数还是有技巧的,如图:
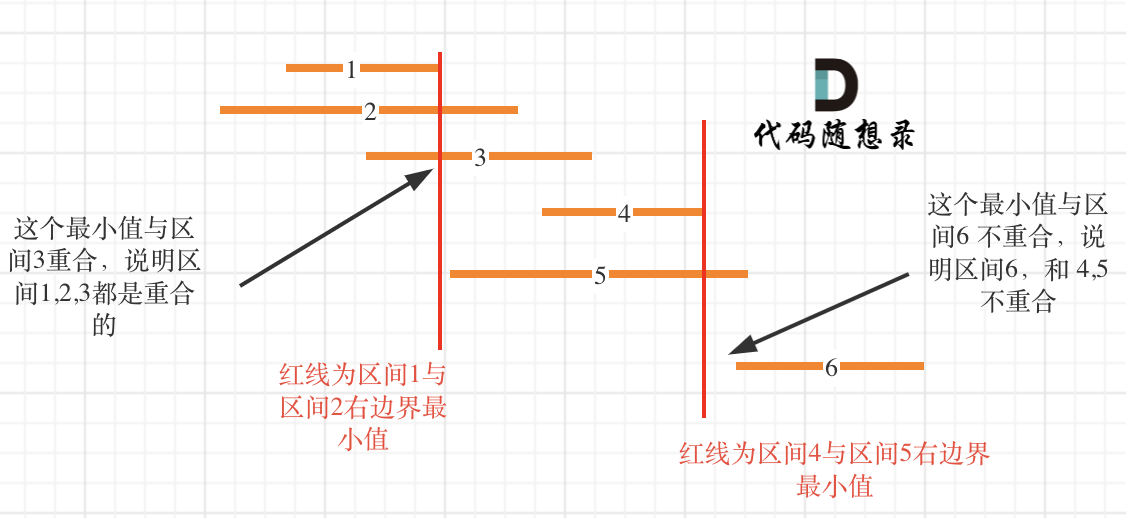
区间,1,2,3,4,5,6都按照右边界排好序。
当确定区间 1 和 区间2 重叠后,如何确定是否与 区间3 也重贴呢?
就是取 区间1 和 区间2 右边界的最小值,因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分,如果这个最小值也触达到区间3,那么说明 区间 1,2,3都是重合的。
接下来就是找大于区间1结束位置的区间,是从区间4开始。那有同学问了为什么不从区间5开始?别忘了已经是按照右边界排序的了。
区间4结束之后,再找到区间6,所以一共记录非交叉区间的个数是三个。
总共区间个数为6,减去非交叉区间的个数3。移除区间的最小数量就是3。
C++代码如下:
class Solution {
public:
// 按照区间右边界排序
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[1] < b[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 1; // 记录非交叉区间的个数
int end = intervals[0][1]; // 记录区间分割点
for (int i = 1; i < intervals.size(); i++) {
if (end <= intervals[i][0]) {
end = intervals[i][1];
count++;
}
}
return intervals.size() - count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- 时间复杂度:O(nlog n) ,有一个快排
- 空间复杂度:O(n),有一个快排,最差情况(倒序)时,需要n次递归调用。因此确实需要O(n)的栈空间
大家此时会发现如此复杂的一个问题,代码实现却这么简单!
# 补充
# 补充(1)
左边界排序可不可以呢?
也是可以的,只不过 左边界排序我们就是直接求 重叠的区间,count为记录重叠区间数。
class Solution {
public:
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[0] < b[0]; // 改为左边界排序
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 0; // 注意这里从0开始,因为是记录重叠区间
int end = intervals[0][1]; // 记录区间分割点
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= end) end = intervals[i][1]; // 无重叠的情况
else { // 重叠情况
end = min(end, intervals[i][1]);
count++;
}
}
return count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
其实代码还可以精简一下, 用 intervals[i][1] 替代 end变量,只判断 重叠情况就好
class Solution {
public:
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[0] < b[0]; // 改为左边界排序
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 0; // 注意这里从0开始,因为是记录重叠区间
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] < intervals[i - 1][1]) { //重叠情况
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]);
count++;
}
}
return count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 补充(2)
本题其实和452.用最少数量的箭引爆气球 (opens new window)非常像,弓箭的数量就相当于是非交叉区间的数量,只要把弓箭那道题目代码里射爆气球的判断条件加个等号(认为[0,1][1,2]不是相邻区间),然后用总区间数减去弓箭数量 就是要移除的区间数量了。
把452.用最少数量的箭引爆气球 (opens new window)代码稍做修改,就可以AC本题。
class Solution {
public:
// 按照区间右边界排序
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[1] < b[1]; // 右边界排序
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int result = 1; // points 不为空至少需要一支箭
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= intervals[i - 1][1]) {
result++; // 需要一支箭
}
else { // 气球i和气球i-1挨着
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // 更新重叠气球最小右边界
}
}
return intervals.size() - result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
这里按照 左边界排序,或者按照右边界排序,都可以AC,原理是一样的。
class Solution {
public:
// 按照区间左边界排序
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[0] < b[0]; // 左边界排序
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int result = 1; // points 不为空至少需要一支箭
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= intervals[i - 1][1]) {
result++; // 需要一支箭
}
else { // 气球i和气球i-1挨着
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // 更新重叠气球最小右边界
}
}
return intervals.size() - result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 其他语言版本
# Java
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a,b)-> {
return Integer.compare(a[0],b[0]);
});
int count = 1;
for(int i = 1;i < intervals.length;i++){
if(intervals[i][0] < intervals[i-1][1]){
intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);
continue;
}else{
count++;
}
}
return intervals.length - count;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
按左边排序,不管右边顺序。相交的时候取最小的右边。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a,b)-> {
return Integer.compare(a[0],b[0]);
});
int remove = 0;
int pre = intervals[0][1];
for(int i = 1; i < intervals.length; i++) {
if(pre > intervals[i][0]) {
remove++;
pre = Math.min(pre, intervals[i][1]);
}
else pre = intervals[i][1];
}
return remove;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Python
贪心 基于左边界
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if not intervals:
return 0
intervals.sort(key=lambda x: x[0]) # 按照左边界升序排序
count = 0 # 记录重叠区间数量
for i in range(1, len(intervals)):
if intervals[i][0] < intervals[i - 1][1]: # 存在重叠区间
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]) # 更新重叠区间的右边界
count += 1
return count
2
3
4
5
6
7
8
9
10
11
12
13
14
15
贪心 基于左边界 把452.用最少数量的箭引爆气球代码稍做修改
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if not intervals:
return 0
intervals.sort(key=lambda x: x[0]) # 按照左边界升序排序
result = 1 # 不重叠区间数量,初始化为1,因为至少有一个不重叠的区间
for i in range(1, len(intervals)):
if intervals[i][0] >= intervals[i - 1][1]: # 没有重叠
result += 1
else: # 重叠情况
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]) # 更新重叠区间的右边界
return len(intervals) - result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Go
func eraseOverlapIntervals(intervals [][]int) int {
sort.Slice(intervals, func(i, j int) bool {
return intervals[i][1] < intervals[j][1]
})
res := 1
for i := 1; i < len(intervals); i++ {
if intervals[i][0] >= intervals[i-1][1] {
res++
} else {
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1])
}
}
return len(intervals) - res
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# JavaScript
- 按右边界排序
var eraseOverlapIntervals = function(intervals) {
intervals.sort((a, b) => {
return a[1] - b[1]
})
let count = 1
let end = intervals[0][1]
for(let i = 1; i < intervals.length; i++) {
let interval = intervals[i]
if(interval[0] >= end) {
end = interval[1]
count += 1
}
}
return intervals.length - count
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- 按左边界排序
var eraseOverlapIntervals = function(intervals) {
// 按照左边界升序排列
intervals.sort((a, b) => a[0] - b[0])
let count = 1
let end = intervals[intervals.length - 1][0]
// 倒序遍历,对单个区间来说,左边界越大越好,因为给前面区间的空间越大
for(let i = intervals.length - 2; i >= 0; i--) {
if(intervals[i][1] <= end) {
count++
end = intervals[i][0]
}
}
// count 记录的是最大非重复区间的个数
return intervals.length - count
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# TypeScript
按右边界排序,从左往右遍历
function eraseOverlapIntervals(intervals: number[][]): number {
const length = intervals.length;
if (length === 0) return 0;
intervals.sort((a, b) => a[1] - b[1]);
let right: number = intervals[0][1];
let count: number = 1;
for (let i = 1; i < length; i++) {
if (intervals[i][0] >= right) {
count++;
right = intervals[i][1];
}
}
return length - count;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
按左边界排序,从左往右遍历
function eraseOverlapIntervals(intervals: number[][]): number {
if (intervals.length === 0) return 0;
intervals.sort((a, b) => a[0] - b[0]);
let right: number = intervals[0][1];
let tempInterval: number[];
let resCount: number = 0;
for (let i = 1, length = intervals.length; i < length; i++) {
tempInterval = intervals[i];
if (tempInterval[0] >= right) {
// 未重叠
right = tempInterval[1];
} else {
// 有重叠,移除当前interval和前一个interval中右边界更大的那个
right = Math.min(right, tempInterval[1]);
resCount++;
}
}
return resCount;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Scala
object Solution {
def eraseOverlapIntervals(intervals: Array[Array[Int]]): Int = {
var result = 0
var interval = intervals.sortWith((a, b) => {
a(1) < b(1)
})
var edge = Int.MinValue
for (i <- 0 until interval.length) {
if (edge <= interval(i)(0)) {
edge = interval(i)(1)
} else {
result += 1
}
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Rust
impl Solution {
pub fn erase_overlap_intervals(mut intervals: Vec<Vec<i32>>) -> i32 {
if intervals.is_empty() {
return 0;
}
intervals.sort_by_key(|interval| interval[1]);
let mut count = 1;
let mut end = intervals[0][1];
for v in intervals.iter().skip(1) {
if end <= v[0] {
end = v[1];
count += 1;
}
}
(intervals.len() - count) as i32
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# C
// 按照区间右边界排序
int cmp(const void * var1, const void * var2){
return (*(int **) var1)[1] - (*(int **) var2)[1];
}
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize) {
if(intervalsSize == 0){
return 0;
}
qsort(intervals, intervalsSize, sizeof (int *), cmp);
// 记录非重叠的区间数量
int count = 1;
// 记录区间分割点
int end = intervals[0][1];
for(int i = 1; i < intervalsSize; i++){
if(end <= intervals[i][0]){
end = intervals[i][1];
count++;
}
}
return intervalsSize - count;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C#
public class Solution
{
public int EraseOverlapIntervals(int[][] intervals)
{
if (intervals.Length == 0) return 0;
Array.Sort(intervals, (a, b) => a[1].CompareTo(b[1]));
int res = 1, end = intervals[0][1];
for (int i = 1; i < intervals.Length; i++)
{
if (end <= intervals[i][0])
{
end = intervals[i][1];
res++;
}
}
return intervals.Length - res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

评论
验证登录状态...