代码随想录

# 右旋字符串

卡码网题目链接 (opens new window)

字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k，请编写一个函数，将字符串中的后面 k 个字符移到字符串的前面，实现字符串的右旋转操作。

例如，对于输入字符串 "abcdefg" 和整数 2，函数应该将其转换为 "fgabcde"。

输入：输入共包含两行，第一行为一个正整数 k，代表右旋转的位数。第二行为字符串 s，代表需要旋转的字符串。

输出：输出共一行，为进行了右旋转操作后的字符串。

样例输入：

2
abcdefg
1
2

样例输出：

fgabcde
1

数据范围：1 <= k < 10000, 1 <= s.length < 10000;

# 思路

为了让本题更有意义，提升一下本题难度：不能申请额外空间，只能在本串上操作。 （Java不能在字符串上修改，所以使用java一定要开辟新空间）

不能使用额外空间的话，模拟在本串操作要实现右旋转字符串的功能还是有点困难的。

那么我们可以想一下上一题目字符串：花式反转还不够！ (opens new window)中讲过，使用整体反转+局部反转就可以实现反转单词顺序的目的。

本题中，我们需要将字符串右移n位，字符串相当于分成了两个部分，如果n为2，符串相当于分成了两个部分，如图： （length为字符串长度）

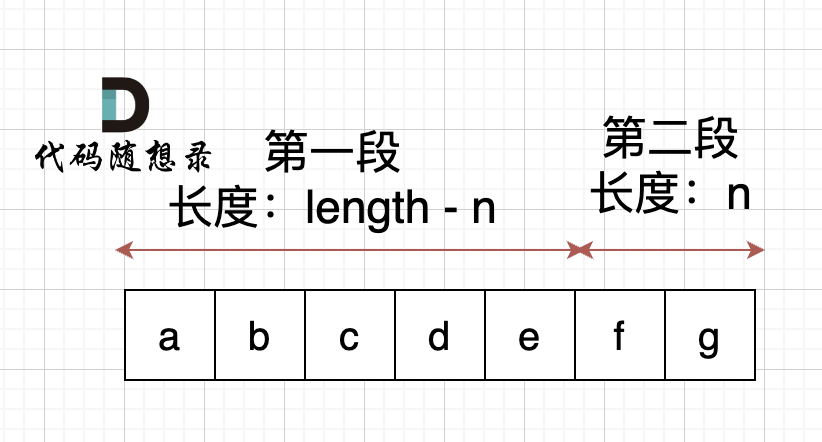
右移n位， 就是将第二段放在前面，第一段放在后面，先不考虑里面字符的顺序，是不是整体倒叙不就行了。如图：

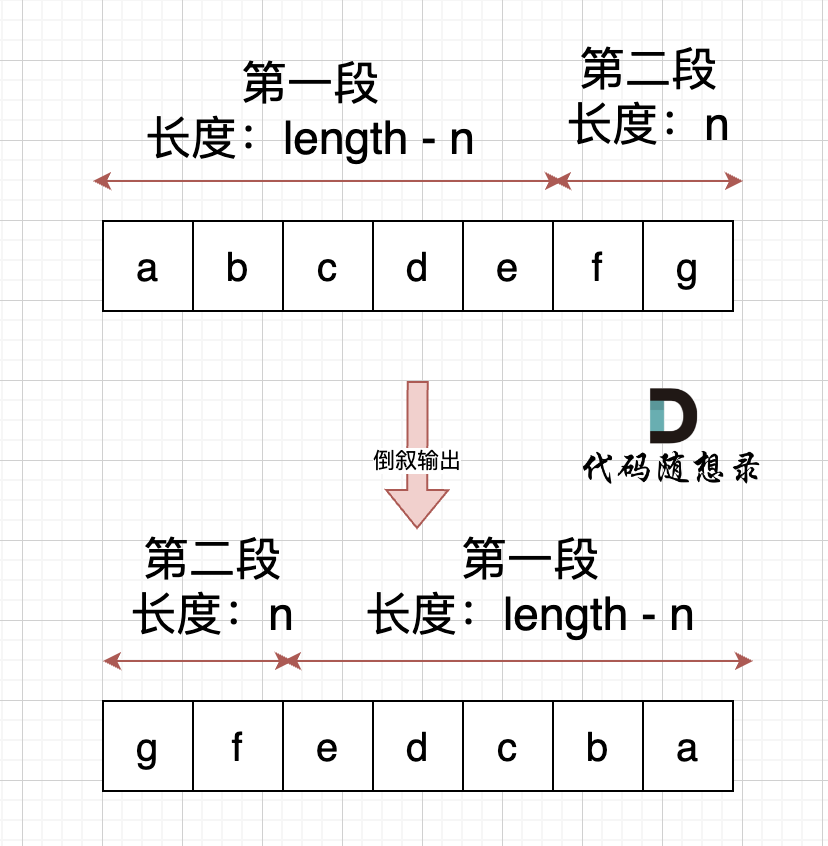
此时第一段和第二段的顺序是我们想要的，但里面的字符位置被我们倒叙，那么此时我们在把 第一段和第二段里面的字符再倒叙一把，这样字符顺序不就正确了。 如果：

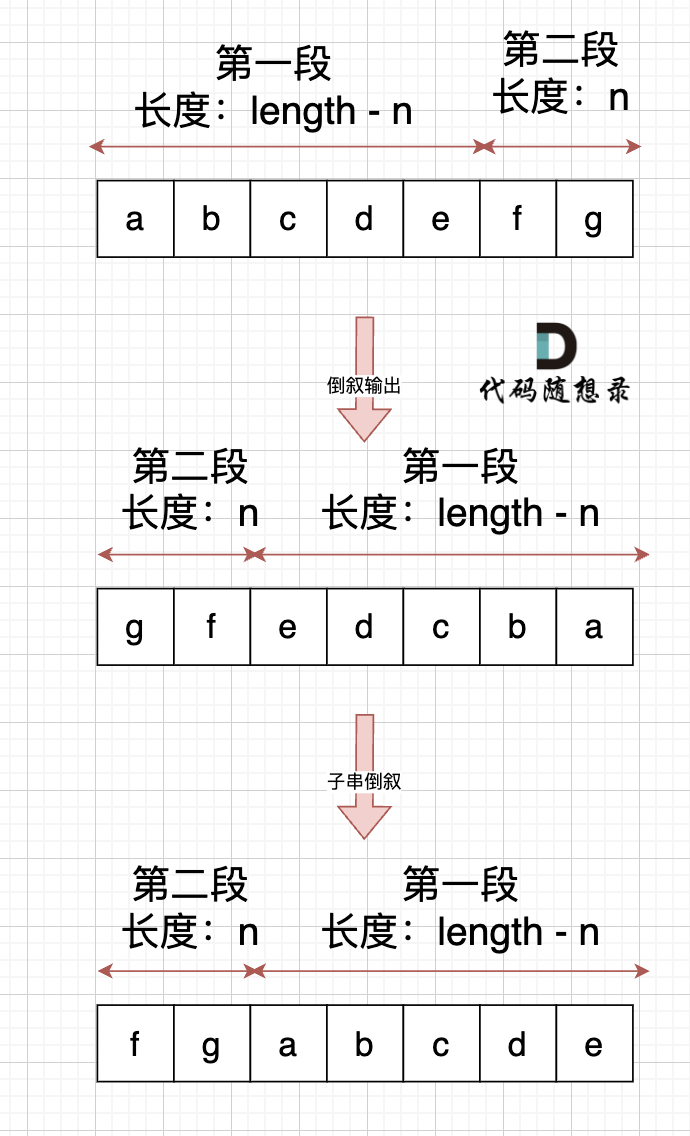
其实，思路就是 通过 整体倒叙，把两段子串顺序颠倒，两个段子串里的的字符在倒叙一把，负负得正，这样就不影响子串里面字符的顺序了。

整体代码如下：

// 版本一
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); //获取长度

    reverse(s.begin(), s.end()); // 整体反转
    reverse(s.begin(), s.begin() + n); // 先反转前一段，长度n
    reverse(s.begin() + n, s.end()); // 再反转后一段

    cout << s << endl;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

那么整体反正的操作放在下面，先局部反转行不行？

可以的，不过，要记得 控制好 局部反转的长度，如果先局部反转，那么先反转的子串长度就是 len - n，如图：

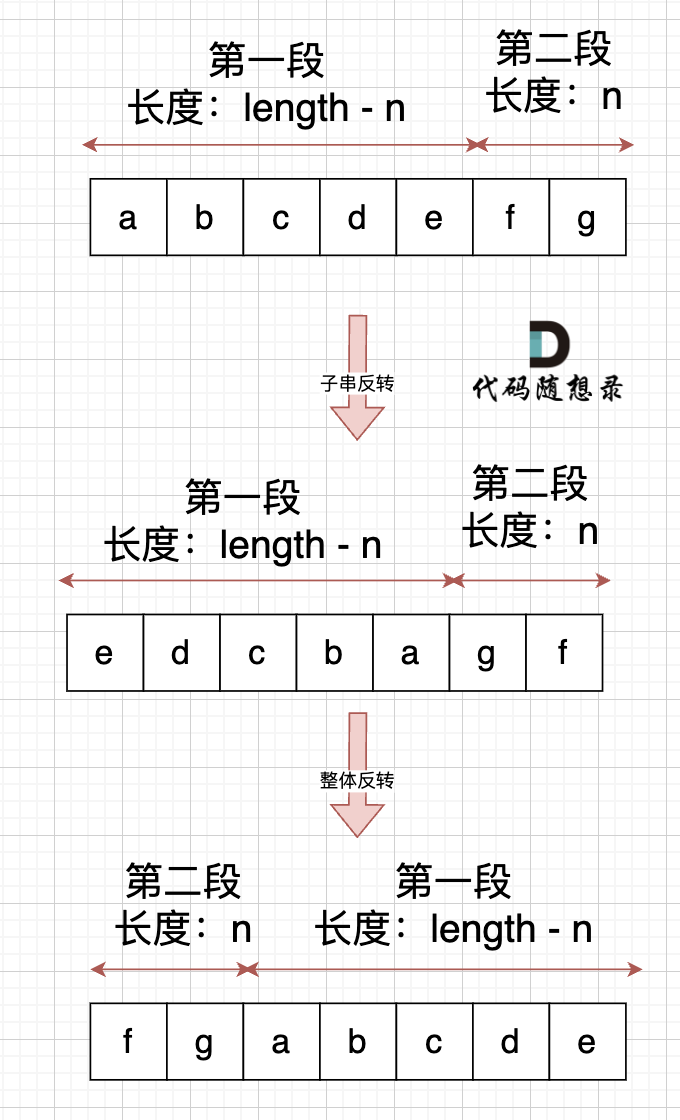
代码如下：

// 版本二 
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); //获取长度
    reverse(s.begin(), s.begin() + len - n); // 先反转前一段，长度len-n ，注意这里是和版本一的区别
    reverse(s.begin() + len - n, s.end()); // 再反转后一段
    reverse(s.begin(), s.end()); // 整体反转
    cout << s << endl;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 拓展

大家在做剑指offer的时候，会发现 剑指offer的题目是左反转，那么左反转和右反转 有什么区别呢？

其实思路是一样一样的，就是反转的区间不同而已。如果本题是左旋转n，那么实现代码如下：

#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int n;
    string s;
    cin >> n;
    cin >> s;
    int len = s.size(); //获取长度
    reverse(s.begin(), s.begin() + n); //  反转第一段长度为n 
    reverse(s.begin() + n, s.end()); // 反转第二段长度为len-n 
    reverse(s.begin(), s.end());  // 整体反转
    cout << s << endl;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

大家可以感受一下 这份代码和 版本二的区别， 其实就是反转的区间不同而已。

那么左旋转的话，可以不可以先整体反转，例如想版本一的那样呢？

当然可以。

# 其他语言版本

# Java：

// 版本一
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = Integer.parseInt(in.nextLine());
        String s = in.nextLine();

        int len = s.length();  //获取字符串长度
        char[] chars = s.toCharArray();
        reverseString(chars, 0, len - 1);  //反转整个字符串
        reverseString(chars, 0, n - 1);  //反转前一段字符串，此时的字符串首尾尾是0,n - 1
        reverseString(chars, n, len - 1);  //反转后一段字符串，此时的字符串首尾尾是n,len - 1
        
        System.out.println(chars);

    }

    public static void reverseString(char[] ch, int start, int end) {
        //异或法反转字符串，参照题目 344.反转字符串的解释
        while (start < end) {
            ch[start] ^= ch[end];
            ch[end] ^= ch[start];
            ch[start] ^= ch[end];
            start++;
            end--;
        }
    }
}


// 版本二
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = Integer.parseInt(in.nextLine());
        String s = in.nextLine();

        int len = s.length();  //获取字符串长度
        char[] chars = s.toCharArray();
        reverseString(chars, 0, len - n - 1);  //反转前一段字符串，此时的字符串首尾是0,len - n - 1
        reverseString(chars, len - n, len - 1);  //反转后一段字符串，此时的字符串首尾是len - n,len - 1
        reverseString(chars, 0, len - 1);  //反转整个字符串

        System.out.println(chars);

    }

    public static void reverseString(char[] ch, int start, int end) {
        //异或法反转字符串，参照题目 344.反转字符串的解释
        while (start < end) {
            ch[start] ^= ch[end];
            ch[end] ^= ch[start];
            ch[start] ^= ch[end];
            start++;
            end--;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

# Python:

#获取输入的数字k和字符串
k = int(input())
s = input()

#通过切片反转第一段和第二段字符串
#注意：python中字符串是不可变的，所以也需要额外空间
s = s[len(s)-k:] + s[:len(s)-k]
print(s)
1
2
3
4
5
6
7
8
k = int(input())
s = input()

print(s[-k:] + s[:-k])
1
2
3
4

# Go：

package main
import "fmt"

func reverse (strByte []byte, l, r int){
    for l < r {
        strByte[l], strByte[r] = strByte[r], strByte[l]
        l++
        r--
    }
}


func main(){
    var str string
    var target int
    
    fmt.Scanln(&target)
    fmt.Scanln(&str)
    strByte := []byte(str)
    
    reverse(strByte, 0, len(strByte) - 1)
    reverse(strByte, 0, target - 1)
    reverse(strByte, target, len(strByte) - 1)
    
    fmt.Printf(string(strByte))
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# C：

#include <stdio.h>
#include <string.h>

void reverse(char *s, int left, int right)
{
    while(left <= right)
    {
        char c = s[left];
        s[left] = s[right];
        s[right] = c;
        left++;
        right--;
    }
}

void rightRotate(char *s, int k)
{
    int len = strlen(s);
    // 先局部反转再整体反转
    reverse(s, 0, len - k - 1);   // 反转前部分
    reverse(s, len - k, len - 1); // 反转后部分：后k位
    reverse(s, 0, len - 1);       // 整体反转
}

int main()
{

    int k;
    scanf("%d", &k);
    char s[10000];
    scanf("%s", s);

    rightRotate(s, k);
    printf("%s\n", s);

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# JavaScript：

// JS中字符串内不可单独修改

const readline = require('readline')

const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout
})

const inputs = []; // 存储输入

rl.on('line', function(data) {
    inputs.push(data);

}).on('close', function() {
    const res = deal(inputs);
    // 打印结果
    console.log(res);
})

// 对传入的数据进行处理
function deal(inputs) {
    let [k, s] = inputs;
    const len = s.length - 1;
    k = parseInt(k);
    str = s.split('');
    
    str = reverseStr(str, 0, len - k)
    str = reverseStr(str, len - k + 1, len)
    str = reverseStr(str, 0, len)

    return str.join('');
}

// 根据提供的范围进行翻转
function reverseStr(s, start, end) {
    
    while (start < end) {
        [s[start], s[end]] = [s[end], s[start]]
        
        start++;
        end--;
    }

    return s;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# TypeScript：

# Swift:

# PHP：

<?php
// 反转函数
function reverse(&$s, $start, $end) {
    for ($i = $start, $j = $end; $i < $j; $i++, $j--) {
        $tmp = $s[$i];
        $s[$i] = $s[$j];
        $s[$j] = $tmp;
    }
}
    
// 标准输入：读取右旋转位数和字符串    
$n = trim(fgets(STDIN));
$s = trim(fgets(STDIN));
// 字符串长度
$len = strlen($s);
// 先部分反转
reverse($s, $len - $n, $len - 1);
reverse($s, 0, $len - $n - 1);
// 再整体反转
reverse($s, 0, $len - 1);

echo $s;
?>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Scala:

# Rust:

上次更新：: 8/22/2024, 9:07:28 PM

← 6. 实现strStr()) →

@2021-2024 代码随想录 版权所有 粤ICP备19156078号