参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

# 1020. 飞地的数量

力扣链接 (opens new window)

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次移动是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

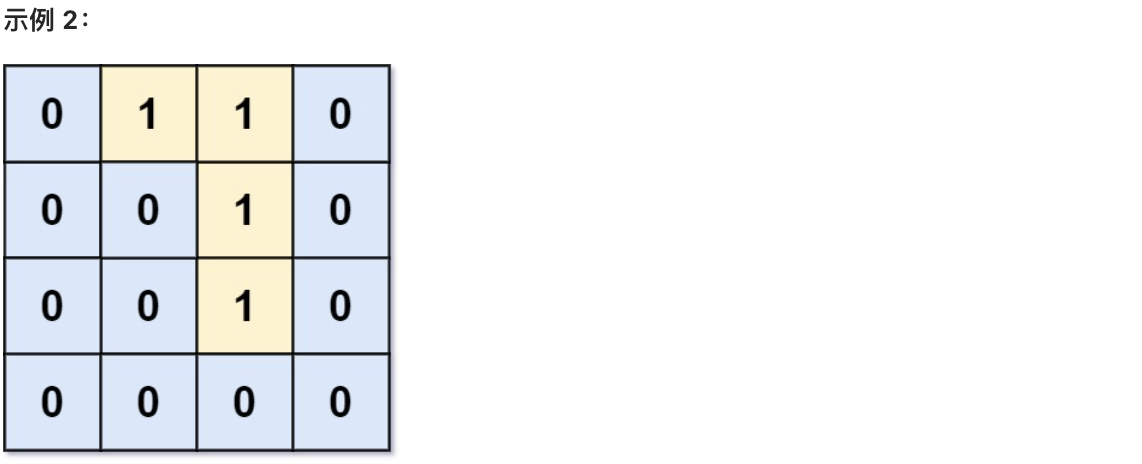
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

# 思路

本题使用dfs，bfs，并查集都是可以的。

本题要求找到不靠边的陆地面积，那么我们只要从周边找到陆地然后通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋，然后再去重新遍历地图的时候，统计此时还剩下的陆地就可以了。

如图，在遍历地图周围四个边，靠地图四边的陆地，都为绿色，

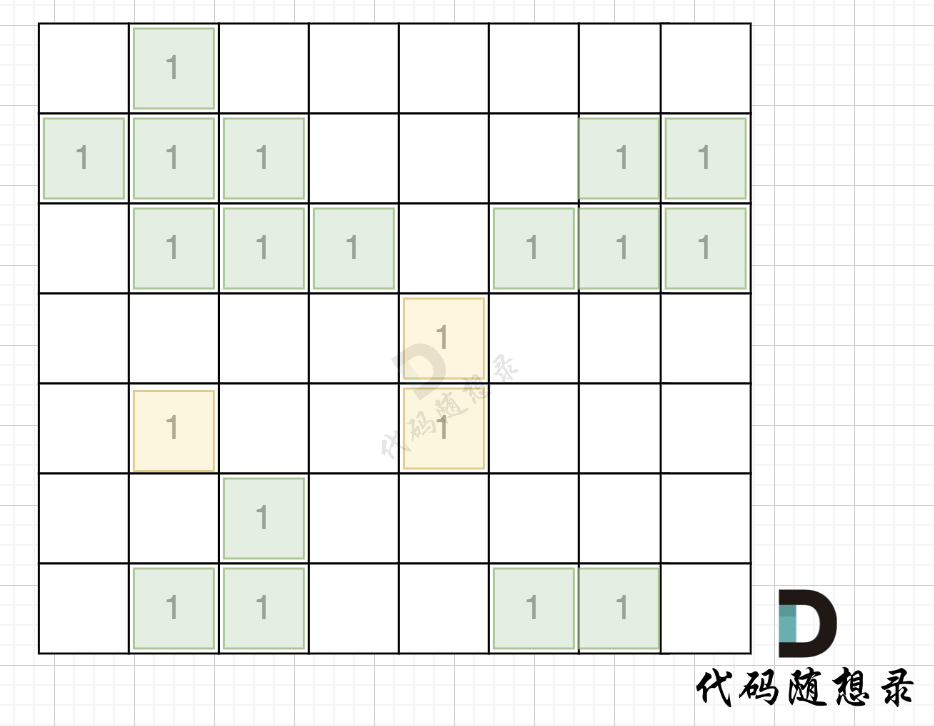
在遇到地图周边陆地的时候，将1都变为0，此时地图为这样：

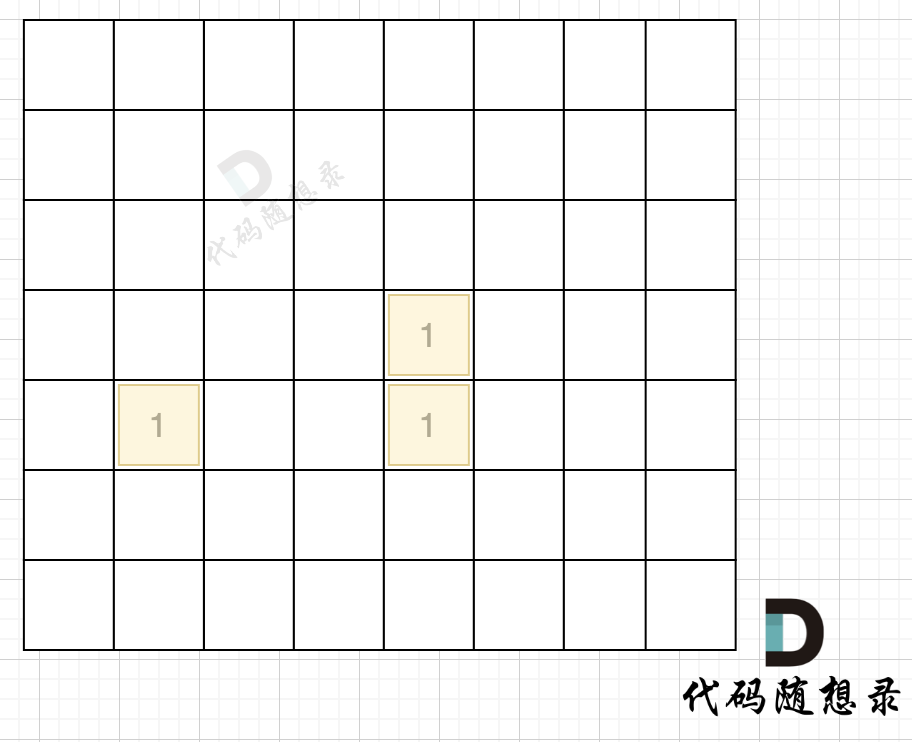
然后我们再去遍历这个地图，遇到有陆地的地方，去采用深搜或者广搜，边统计所有陆地。

如果对深搜或者广搜不够了解，建议先看这里：深度优先搜索精讲 (opens new window)，广度优先搜索精讲 (opens new window)。

采用深度优先搜索的代码如下：

class Solution {
private:
    int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
    int count; // 统计符合题目要求的陆地空格数量
    void dfs(vector<vector<int>>& grid, int x, int y) {
        grid[x][y] = 0;
        count++;
        for (int i = 0; i < 4; i++) { // 向四个方向遍历
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            // 超过边界
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
            // 不符合条件，不继续遍历
            if (grid[nextx][nexty] == 0) continue;

            dfs (grid, nextx, nexty);
        }
        return;
    }

public:
    int numEnclaves(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        // 从左侧边，和右侧边 向中间遍历
        for (int i = 0; i < n; i++) {
            if (grid[i][0] == 1) dfs(grid, i, 0);
            if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
        }
        // 从上边和下边 向中间遍历
        for (int j = 0; j < m; j++) {
            if (grid[0][j] == 1) dfs(grid, 0, j);
            if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
        }
        count = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 1) dfs(grid, i, j);
            }
        }
        return count;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

采用广度优先搜索的代码如下：

class Solution {
private:
int count = 0;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<int>>& grid, int x, int y) {
    queue<pair<int, int>> que;
    que.push({x, y});
    grid[x][y] = 0; // 只要加入队列，立刻标记
    count++;
    while(!que.empty()) {
        pair<int ,int> cur = que.front(); que.pop();
        int curx = cur.first;
        int cury = cur.second;
        for (int i = 0; i < 4; i++) {
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1];
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
            if (grid[nextx][nexty] == 1) {
                que.push({nextx, nexty});
                count++;
                grid[nextx][nexty] = 0; // 只要加入队列立刻标记
            }
        }
    }

}

public:
    int numEnclaves(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        // 从左侧边，和右侧边 向中间遍历
        for (int i = 0; i < n; i++) {
            if (grid[i][0] == 1) bfs(grid, i, 0);
            if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
        }
        // 从上边和下边 向中间遍历
        for (int j = 0; j < m; j++) {
            if (grid[0][j] == 1) bfs(grid, 0, j);
            if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
        }
        count = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 1) bfs(grid, i, j);
            }
        }
        return count;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# 其他语言版本

# Java

深度优先遍历(没有终止条件 + 空間優化（淹沒島嶼，沒有使用visited數組）)

//DFS
class Solution {
    int count = 0;
    int[][] dir ={
        {0, 1},
        {1, 0},
        {-1, 0},
        {0, -1}
    };
    private void dfs(int[][] grid, int x, int y){
        if(grid[x][y] == 0)
            return;
        
        grid[x][y] = 0;
        count++;

        for(int i = 0; i < 4; i++){
            int nextX = x + dir[i][0];
            int nextY = y + dir[i][1];

            if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
                continue;
            dfs(grid, nextX, nextY);
        }
        
    }

    public int numEnclaves(int[][] grid) {
        for(int i = 0; i < grid.length; i++){
            if(grid[i][0] == 1)
                dfs(grid, i, 0);
            if(grid[i][grid[0].length - 1] == 1)
                dfs(grid, i, grid[0].length - 1);
        }
        //初始化的時候，j 的上下限有調整過，必免重複操作。
        for(int j = 1; j < grid[0].length - 1; j++){
            if(grid[0][j] == 1)
                dfs(grid, 0, j);
            if(grid[grid.length - 1][j] == 1)
                dfs(grid, grid.length - 1, j);
        }
        count = 0;

        for(int i = 1; i < grid.length - 1; i++){
            for(int j = 1; j < grid[0].length - 1; j++){
                if(grid[i][j] == 1)
                    dfs(grid, i, j);
            }
        }
        return count;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

深度优先遍历(没有终止条件)

class Solution {
    // 四个方向
    private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};

    // 深度优先遍历，把可以通向边缘部分的 1 全部标记成 true
    public void dfs(int[][] grid, int row, int col, boolean[][] visited) {
        for (int[] current: position) {
            int newRow = row + current[0], newCol = col + current[1];
            // 下标越界直接跳过
            if (newRow < 0 || newRow >= grid.length || newCol < 0 || newCol >= grid[0].length) continue;
            // 当前位置不是 1 或者已经被访问了就直接跳过
            if (grid[newRow][newCol] != 1 || visited[newRow][newCol]) continue;
            visited[newRow][newCol] = true;
            dfs(grid, newRow, newCol, visited);
        }
    }

    public int numEnclaves(int[][] grid) {
        int rowSize = grid.length, colSize = grid[0].length, ans = 0;	// ans 记录答案
        // 标记数组记录每个值为 1 的位置是否可以到达边界，可以为 true，反之为 false
        boolean[][] visited = new boolean[rowSize][colSize];
        // 左侧边界和右侧边界查找 1 进行标记并进行深度优先遍历
        for (int row = 0; row < rowSize; row++) {
            if (grid[row][0] == 1 && !visited[row][0]) {
                visited[row][0] = true;
                dfs(grid, row, 0, visited);
            }
            if (grid[row][colSize - 1] == 1 && !visited[row][colSize - 1]) {
                visited[row][colSize - 1] = true;
                dfs(grid, row, colSize - 1, visited);
            }
        }
        // 上边界和下边界遍历，但是四个角不用遍历，因为上面已经遍历到了
        for (int col = 1; col < colSize - 1; col++) {
            if (grid[0][col] == 1 && !visited[0][col]) {
                visited[0][col] = true;
                dfs(grid, 0, col, visited);
            }
            if (grid[rowSize - 1][col] == 1 && !visited[rowSize - 1][col]) {
                visited[rowSize - 1][col] = true;
                dfs(grid, rowSize - 1, col, visited);
            }
        }
        // 查找没有标记过的 1，记录到 ans 中
        for (int row = 0; row < rowSize; row++) {
            for (int col = 0; col < colSize; col++) {
                if (grid[row][col] == 1 && !visited[row][col]) ++ans;
            }
        }
        return ans;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

广度优先遍历（使用visited數組）

class Solution {
    // 四个方向
    private static final int[][] position = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};

    // 广度优先遍历，把可以通向边缘部分的 1 全部标记成 true
    public void bfs(int[][] grid, Queue<int[]> queue, boolean[][] visited) {
        while (!queue.isEmpty()) {
            int[] curPos = queue.poll();
            for (int[] current: position) {
                int row = curPos[0] + current[0], col = curPos[1] + current[1];
                // 下标越界直接跳过
                if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length) 
                    continue;
                // 当前位置不是 1 或者已经被访问了就直接跳过
                if (visited[row][col] || grid[row][col] == 0) continue;
                visited[row][col] = true;
                queue.add(new int[]{row, col});
            }
        }
    }

    public int numEnclaves(int[][] grid) {
        int rowSize = grid.length, colSize = grid[0].length, ans = 0;	// ans 记录答案
        // 标记数组记录每个值为 1 的位置是否可以到达边界，可以为 true，反之为 false
        boolean[][] visited = new boolean[rowSize][colSize];
        Queue<int[]> queue = new ArrayDeque<>();
        // 搜索左侧边界和右侧边界查找 1 存入队列
        for (int row = 0; row < rowSize; row++) {
            if (grid[row][0] == 1) {
                visited[row][0] = true;
                queue.add(new int[]{row, 0});
            }
            if (grid[row][colSize - 1] == 1) {
                visited[row][colSize - 1] = true;
                queue.add(new int[]{row, colSize - 1});
            }
        }
        // 搜索上边界和下边界遍历，但是四个角不用遍历，因为上面已经遍历到了
        for (int col = 1; col < colSize - 1; col++) {
            if (grid[0][col] == 1) {
                visited[0][col] = true;
                queue.add(new int[]{0, col});
            }
            if (grid[rowSize - 1][col] == 1 && !visited[rowSize - 1][col]) {
                visited[rowSize - 1][col] = true;
                queue.add(new int[]{rowSize - 1, col});
            }
        }
        bfs(grid, queue, visited);		// 广度优先遍历
        // 查找没有标记过的 1，记录到 ans 中
        for (int row = 0; row < rowSize; row++) {
            for (int col = 0; col < colSize; col++) {
                if (grid[row][col] == 1 && !visited[row][col]) ++ans;
            }
        }
        return ans;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

廣度优先遍历(空間優化（淹沒島嶼，沒有使用visited數組）)

//BFS
class Solution {
    int count = 0;
    int[][] dir ={
        {0, 1},
        {1, 0},
        {-1, 0},
        {0, -1}
    };
    private void bfs(int[][] grid, int x, int y){
        Queue<Integer> que = new LinkedList<>();
        que.offer(x);
        que.offer(y);
        count++;
        grid[x][y] = 0;
        
        while(!que.isEmpty()){
            int currX = que.poll();
            int currY = que.poll();

            for(int i = 0; i < 4; i++){
                int nextX = currX + dir[i][0];
                int nextY = currY + dir[i][1];

                if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
                    continue;

                if(grid[nextX][nextY] == 1){
                    que.offer(nextX);
                    que.offer(nextY);
                    count++;
                    grid[nextX][nextY] = 0;
                }
            }
        }
    }

    public int numEnclaves(int[][] grid) {
        for(int i = 0; i < grid.length; i++){
            if(grid[i][0] == 1)
                bfs(grid, i, 0);
            if(grid[i][grid[0].length - 1] == 1)
                bfs(grid, i, grid[0].length - 1);
        }
        for(int j = 1; j < grid[0].length; j++){
            if(grid[0][j] == 1)
                bfs(grid, 0 , j);
            if(grid[grid.length - 1][j] == 1)
                bfs(grid, grid.length - 1, j);
        }
        count = 0;
        for(int i = 1; i < grid.length - 1; i++){
            for(int j = 1; j < grid[0].length - 1; j++){
                if(grid[i][j] == 1)
                    bfs(grid,i ,j);
            }
        }
        return count;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

# Python

深度优先遍历

class Solution:
    def __init__(self):
        self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]]	# 四个方向

    # 深度优先遍历，把可以通向边缘部分的 1 全部标记成 true
    def dfs(self, grid: List[List[int]], row: int, col: int, visited: List[List[bool]]) -> None:
        for current in self.position:
            newRow, newCol = row + current[0], col + current[1]
            # 索引下标越界
            if newRow < 0 or newRow >= len(grid) or newCol < 0 or newCol >= len(grid[0]): 
                continue
            # 当前位置值不是 1 或者已经被访问过了
            if grid[newRow][newCol] == 0 or visited[newRow][newCol]: continue
            visited[newRow][newCol] = True
            self.dfs(grid, newRow, newCol, visited)

    def numEnclaves(self, grid: List[List[int]]) -> int:
        rowSize, colSize, ans = len(grid), len(grid[0]), 0
        # 标记数组记录每个值为 1 的位置是否可以到达边界，可以为 True，反之为 False
        visited = [[False for _ in range(colSize)] for _ in range(rowSize)]
        # 搜索左边界和右边界，对值为 1 的位置进行深度优先遍历
        for row in range(rowSize):
            if grid[row][0] == 1:
                visited[row][0] = True
                self.dfs(grid, row, 0, visited)
            if grid[row][colSize - 1] == 1:
                visited[row][colSize - 1] = True
                self.dfs(grid, row, colSize - 1, visited)
        # 搜索上边界和下边界，对值为 1 的位置进行深度优先遍历，但是四个角不需要，因为上面遍历过了
        for col in range(1, colSize - 1):
            if grid[0][col] == 1:
                visited[0][col] = True
                self.dfs(grid, 0, col, visited)
            if grid[rowSize - 1][col] == 1:
                visited[rowSize - 1][col] = True
                self.dfs(grid, rowSize - 1, col, visited)
        # 找出矩阵中值为 1 但是没有被标记过的位置，记录答案
        for row in range(rowSize):
            for col in range(colSize):
                if grid[row][col] == 1 and not visited[row][col]:
                    ans += 1
        return ans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

广度优先遍历

class Solution:
    def __init__(self):
        self.position = [[-1, 0], [0, 1], [1, 0], [0, -1]]	# 四个方向

    # 广度优先遍历，把可以通向边缘部分的 1 全部标记成 true
    def bfs(self, grid: List[List[int]], queue: deque, visited: List[List[bool]]) -> None:
        while queue:
            curPos = queue.popleft()
            for current in self.position:
                row, col = curPos[0] + current[0], curPos[1] + current[1]
                # 索引下标越界
                if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]): continue
                # 当前位置值不是 1 或者已经被访问过了
                if grid[row][col] == 0 or visited[row][col]: continue
                visited[row][col] = True
                queue.append([row, col])


    def numEnclaves(self, grid: List[List[int]]) -> int:
        rowSize, colSize, ans = len(grid), len(grid[0]), 0
        # 标记数组记录每个值为 1 的位置是否可以到达边界，可以为 True，反之为 False
        visited = [[False for _ in range(colSize)] for _ in range(rowSize)]
        queue = deque()		# 队列
        # 搜索左侧边界和右侧边界查找 1 存入队列
        for row in range(rowSize):
            if grid[row][0] == 1:
                visited[row][0] = True
                queue.append([row, 0])
            if grid[row][colSize - 1] == 1:
                visited[row][colSize - 1] = True
                queue.append([row, colSize - 1])
        # 搜索上边界和下边界查找 1 存入队列，但是四个角不用遍历，因为上面已经遍历到了
        for col in range(1, colSize - 1):
            if grid[0][col] == 1:
                visited[0][col] = True
                queue.append([0, col])
            if grid[rowSize - 1][col] == 1:
                visited[rowSize - 1][col] = True
                queue.append([rowSize - 1, col])
        self.bfs(grid, queue, visited)	# 广度优先遍历
        # 找出矩阵中值为 1 但是没有被标记过的位置，记录答案
        for row in range(rowSize):
            for col in range(colSize):
                if grid[row][col] == 1 and not visited[row][col]:
                    ans += 1
        return ans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# Go

dfs:

var DIRECTIONS = [4][2]int{{-1, 0}, {0, -1}, {1, 0}, {0, 1}}
var count int = 0

func numEnclaves(grid [][]int) int {
	rows, cols := len(grid), len(grid[0])
	// 行
	for i := range grid[0] {
		if grid[0][i] == 1 {
			dfs(grid, 0, i)
		}
		if grid[rows-1][i] == 1 {
			dfs(grid, rows-1, i)
		}
	}
	// 列
	for j := range grid {
		if grid[j][0] == 1 {
			dfs(grid, j, 0)
		}
		if grid[j][cols-1] == 1 {
			dfs(grid, j, cols-1)
		}
	}
	count = 0
	for i := range grid {
		for j := range grid[0] {
			if grid[i][j] == 1 {
				dfs(grid, i, j)
			}
		}
	}
	return count
}

func dfs(grid [][]int, i, j int) {
	grid[i][j] = 0
	count++
	for _, d := range DIRECTIONS {
		x, y := i+d[0], j+d[1]
		if x < 0 || x >= len(grid) || y < 0 || y >= len(grid[0]) {
			continue
		}
		if grid[x][y] == 1 {
			dfs(grid, x, y)
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

bfs:

var DIRECTIONS = [4][2]int{{-1, 0}, {0, -1}, {1, 0}, {0, 1}}
var count int = 0

func numEnclaves(grid [][]int) int {
	rows, cols := len(grid), len(grid[0])
	// 行
	for i := range grid[0] {
		if grid[0][i] == 1 {
			bfs(grid, 0, i)
		}
		if grid[rows-1][i] == 1 {
			bfs(grid, rows-1, i)
		}
	}
	// 列
	for j := range grid {
		if grid[j][0] == 1 {
			bfs(grid, j, 0)
		}
		if grid[j][cols-1] == 1 {
			bfs(grid, j, cols-1)
		}
	}
	count = 0
	for i := range grid {
		for j := range grid[0] {
			if grid[i][j] == 1 {
				bfs(grid, i, j)
			}
		}
	}
	return count
}

func bfs(grid [][]int, i, j int) {
	queue := [][]int{}
	queue = append(queue, []int{i, j})
	grid[i][j] = 0
	count++
	for len(queue) > 0 {
		cur := queue[0]
		queue = queue[1:]
		for _, d := range DIRECTIONS {
			x, y := cur[0]+d[0], cur[1]+d[1]
			if x < 0 || x >= len(grid) || y < 0 || y >= len(grid[0]) {
				continue
			}
			if grid[x][y] == 1 {
				count++
				queue = append(queue, []int{x, y})
				grid[x][y] = 0
			}
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

# JavaScript

/**
 * @param {number[][]} grid
 * @return {number}
 */
var numEnclaves = function (grid) {
  let row = grid.length;
  let col = grid[0].length;
  let count = 0;

  // Check the first and last row, if there is a 1, then change all the connected 1s to 0 and don't count them.
  for (let j = 0; j < col; j++) {
    if (grid[0][j] === 1) {
      dfs(0, j, false);
    }
    if (grid[row - 1][j] === 1) {
      dfs(row - 1, j, false);
    }
  }

  // Check the first and last column, if there is a 1, then change all the connected 1s to 0 and don't count them.
  for (let i = 0; i < row; i++) {
    if (grid[i][0] === 1) {
      dfs(i, 0, false);
    }
    if (grid[i][col - 1] === 1) {
      dfs(i, col - 1, false);
    }
  }

  // Check the rest of the grid, if there is a 1, then change all the connected 1s to 0 and count them.
  for (let i = 1; i < row - 1; i++) {
    for (let j = 1; j < col - 1; j++) {
      dfs(i, j, true);
    }
  }

  function dfs(i, j, isCounting) {
    let condition = i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] === 0;

    if (condition) return;
    if (isCounting) count++;

    grid[i][j] = 0;

    dfs(i - 1, j, isCounting);
    dfs(i + 1, j, isCounting);
    dfs(i, j - 1, isCounting);
    dfs(i, j + 1, isCounting);
  }

  return count;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

# Rust

dfs:

impl Solution {
    const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];

    pub fn num_enclaves(mut grid: Vec<Vec<i32>>) -> i32 {
        for i in 0..grid.len() {
            for j in 0..grid[0].len() {
                if (i == 0 || i == grid.len() - 1 || j == 0 || j == grid[0].len() - 1)
                    && grid[i][j] == 1
                {
                    Self::dfs(&mut grid, (i as i32, j as i32));
                }
            }
        }
        grid.iter()
            .map(|nums| nums.iter().filter(|&&num| num == 1).count() as i32)
            .sum()
    }

    pub fn dfs(grid: &mut [Vec<i32>], (x, y): (i32, i32)) {
        grid[x as usize][y as usize] = 0;
        for (dx, dy) in Self::DIRECTIONS {
            let (nx, ny) = (x + dx, y + dy);
            if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
                continue;
            }
            if grid[nx as usize][ny as usize] == 0 {
                continue;
            }
            Self::dfs(grid, (nx, ny));
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

bfs:

use std::collections::VecDeque;
impl Solution {
    const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];

    pub fn num_enclaves(mut grid: Vec<Vec<i32>>) -> i32 {
        for i in 0..grid.len() {
            for j in 0..grid[0].len() {
                if (i == 0 || i == grid.len() - 1 || j == 0 || j == grid[0].len() - 1)
                    && grid[i][j] == 1
                {
                    // Self::dfs(&mut grid, (i as i32, j as i32));
                    Self::bfs(&mut grid, (i as i32, j as i32));
                }
            }
        }
        grid.iter()
            .map(|nums| nums.iter().filter(|&&num| num == 1).count() as i32)
            .sum()
    }

    pub fn bfs(grid: &mut [Vec<i32>], (x, y): (i32, i32)) {
        let mut queue = VecDeque::new();
        queue.push_back((x, y));
        grid[x as usize][y as usize] = 0;
        while let Some((cur_x, cur_y)) = queue.pop_front() {
            for (dx, dy) in Self::DIRECTIONS {
                let (nx, ny) = (cur_x + dx, cur_y + dy);
                if nx < 0 || nx >= grid.len() as i32 || ny < 0 || ny >= grid[0].len() as i32 {
                    continue;
                }

                if grid[nx as usize][ny as usize] == 0 {
                    continue;
                }
                queue.push_back((nx, ny));
                grid[nx as usize][ny as usize] = 0;
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 类似题目

1. 统计封闭岛屿的数目